UFES. Álgebra Linear. Prova 3 Manhã. 2017.2. Questão 1A.
A matriz é simétrica com autovalores , e . Sabemos que e são autovetores de .
(a) Determine os autoespaços de
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Essa parece muito confusa? Já adianto que a ideia por trás não é muito complicada 🙏
Foi dada algumas informações para a gente, como os autovalores e dois autovetores, além de uma informação crucial: A matriz é simétrica!
Você sabe o que é uma matriz simétrica?
Uma matriz simétrica é definida quando a matriz é igual a sua matriz transposta, ou seja
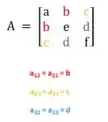
Pela matriz ser simétrica, existe uma propriedade muito bacana que diz que o produto interno de autovetores associados a diferentes autovalores é igual a zero, ou seja, são ortogonais.
O autoespaço de uma matriz, nada mais é que o subespaço formado pelos autovetores da matriz.
Com esse apanhado, podemos começar nossa questãozinha!
Passo 2
Como dito anteriormente, os autovetores associados a diferentes autovalores de uma matriz simétrica são ortogonais e possuem o produto interno igual a zero.
O enunciado nos deu 3 autovalores, sendo 2 valores diferentes: e , vamos verificar se os 2 autovetores são ortogonais.
Como o produto interno entre eles é diferente de , esses dois vetores não são ortogonais, logo, estão associados ao mesmo autovalor.
Mas os autovetores dados estão associados ao autovalor ou ao autovalor ?
Bem, o autovalor aparece duas vezes no enunciado, portanto, os autovetores dados só podem ser associados ao autovalor 3.
Mas como vamos determinar o autovetor associado ao autovalor ?
Passo 3
Se o produto interno de autovetores associados a diferentes autovalores é igual a zero, o autovetor associado ao autovalor deve ser ortogonal a e
Determinando um vetor como o autovetor de e calculando como ortogonal a e , temos para
Para
Montando o sistema, temos
Pela segunda equação, temos que
Substituindo essa informação na primeira equação, temos
Ou seja, temos , e , escrevendo isso em um sistema, temos
ou
Substituindo , nosso autovetor que faltava será
Passo 4
Por fim, como dito anteriormente, o autoespaço de uma matriz é um subespaço formado pelos autovetores da matriz, ou seja, o autoespaço da matriz é formado pelos vetores
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Autoespaço: