Probabilidade e Estatística – PUC RJ – 2019.1 – P4 – Questão 5
Um determinado posto de gasolina vende quatro tipo de produto: etanol, gasolina comum, gasolina aditivada e gasolina premium. Elas custam R$ 1,80, R$ 3,40, R$ 4,00 e R$ 4,80 por galão respectivamente e sejam , , e os consumos desses galões comprados em um dia específico. Suponha que os ’s sejam independentes com:
- Média: , , e ;
- Desvio padrão: , , e .
A receita das vendas é . Suponha que os consumos dos combustíveis seguem uma distribuição normal. Pede-se:
a) Calcule o valor esperada e variância da receita das vendas .
b) Considerando que os valores do item anterior correspondem: e , calcule a probabilidade de a receita das vendas estar entre R$11800 e R$ 12300?
Passo 1
Para resolver esse problema você deve lembrar o seguinte. Considere uma variável :
O valor esperado de será
Já para a variância, temos
É só usar essas expressões que resolvemos o item (a)!
Portanto,
Passo 2
Para o item (b), queremos calcular a probabilidade:
A primeira coisa que devemos olhar é se a distribuição de é normal. Como as distribuições de são normais e a soma de distribuições normais é normal, podemos usar uma distribuição normal para olhar para a variável !
Para resolver esse problema, fazemos a mudança de variável:
Para :
Já para :
Portanto,
Passo 3
Para calcular essa probabilidade, usamos a função probabilidade acumulada:
Olhando na tabela fornecida na prova, é fácil ver que .
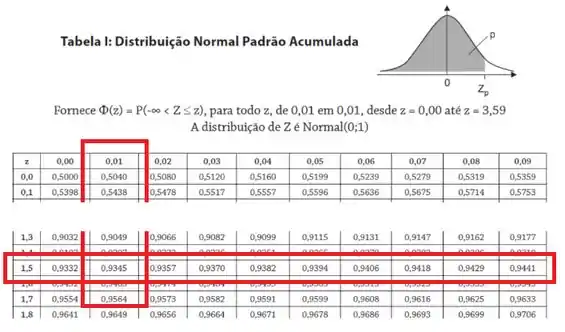
Para achar o trabalho é um pouco mais complicado. Primeiro escrevemos:
Podemos fazer isso pois a distribuição é simétrica em torno de . Além disso,
Portanto,
Partimos para a tabela:
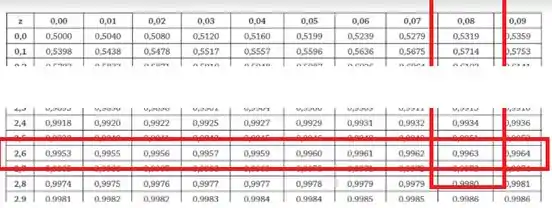
Achamos que , de modo que
Passo 4
Voltando para
Vimos no passo 3 que e , de modo que
Portanto,
Com isso nós fechamos o problema 😊.
Resposta
a) .
b) .