Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Distribuição Normal

Ver Teoria
Exercício 45123456789101112131415161718192021222324252627282930313233343536373839404142434446474849505152535455565758596061626364656667

Enunciado

Tarefa da aula – 5 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 3

Sejam X 1 , X 2 e X 3 os tempos necessários para realizar três reparos sucessivos em determinada oficina. Suponha que sejam variáveis aleatórias normais independentes com valores esperados μ 1 , μ 2 e μ 3 e variâncias σ 1 2 , σ 2 2 e σ 3 2 , respectivamente. Pede-se:

a) Se μ 1   =   μ 2   =   μ 3   =   60 e σ 1 2 = σ 2 2 = σ 3 2 = 15 , calcule P ( X 1   +   X 2   +   X 3   ≤   200 ) e P ( 160   ≤   X 1   +   X 2   +   X 3   ≤   200 ) .

b) Usando os μ i s e σ i s do item anterior, calcule P ( 55   ≤   X - ) e P ( 58   ≤ X - ≤   62 ) .

c) Se μ 1 =   40 , μ 2 =   50 , μ 3 = 60 e σ 1 2 = 10 , σ 2 2 = 12 , σ 3 2 = 14 , calcule P ( X 1   +   X 2   +   X 3   ≤   200 ) e P ( X 1   +   X 2 ≥ 2 X 3 ) .

Passo 1

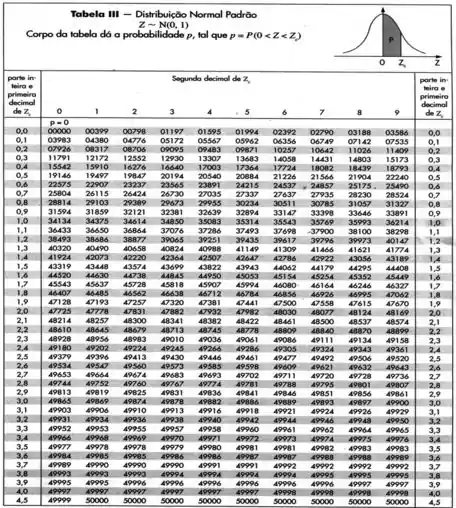
Antes de mais nada, essa é a tabela de distribuição normal pra ajudar na nossa resolução...

a) Bom! Pra essa letra, temos o seguinte...

A média e o desvio padrão são iguais pra X 1 , X 2 e X 3 ...

Desse modo, vamos chamar outra variável aleatória Y ...

Y = X 1 + X 2 + X 3

Como...

μ = μ 1 +   μ 2 +   μ 3   =   180

σ 2 = σ 1 2 +   σ 2 2 + σ 3 2 = 45

Então, peguemos a relação abaixo...

P X 1   +   X 2   +   X 3   ≤   200 = P ( Y ≤ 200 )

Usando...

Z = Y - μ σ

E uma vez que...

σ = 15

Logo;

Z = 200 3 - 60 15 3

Z = 1,333

Ou seja, o que estamos tentando descobrir, na real é...

P Z ≤ 1,333 =   ?

E olhando a tabela, podemos ver que a probabilidade correspondente é de...

ϕ 1,333 = 0,9986

Passo 2

Vamos agora, determinar a probabilidade de P ( 160   ≤   X 1   +   X 2   +   X 3   ≤   200 ) ...

Mas presta atenção numa coisa! Temos três variáveis! E quanto dá 160 / 3 ...

Ora bolas! Dá um valor inferior a média de cada variável! Isso significa que na real estamos calculando a mesma coisa, que é...

P X 1   +   X 2   +   X 3   ≤   200 = P ( Y ≤ 200 )

Cujo resultado é...

ϕ 1,333 = 0,9986

Passo 3

b)

Agora é a vez de calcular separadamente...

Bora calcular primeiro a probabilidade abaixo...

P ( 55   ≤   X - )

E já sabe, né!? Primeiro, achamos Z ...

Z = X - μ σ 2 n

Z = 55 - 60 15 3

Z = - 1

Logo, obtemos que...

P 55   ≤   X - = P - 1   ≤   Z = P   Z ≤ 1   = ϕ ( 1 )

Então, com base na tabela...

ϕ 1 = 0,9015

Passo 4

Para P ( 58   ≤ X - ≤   62 ) , por sua vez...

Z = X - μ σ 2 n

Calculando separadamente...

Z 1 = 58 - 60 3 = - 0,666

Z 2 = 62 - 60 3 = 0,666

Obtemos que...

P 58   ≤ X - ≤   62 =   P - 0,666   ≤ Z ≤   0,666 = 2 ⋅ P Z ≤   0,666 = 2 ϕ ( 0,66 )

P 58   ≤ X - ≤   62 = 0,8357

Passo 5

c)

Pra finalizar, peguemos o caso em que as médias diferem assim como as variâncias...

Nesse caso, a média geral vai ser dada por...

μ = 40 + 50 + 60 3 = 50

E a variância...

σ 2 = 10 + 12 + 14 3 = 12

Calculemos então...

P X 1   +   X 2   +   X 3   ≤   160 = P ( Y ≤ 160 )

Encontrando Z ...

Z = 160 3 - 50 12 3

Z = 0,833

Logo, temos que...

ϕ 0,833 = 0,9525

Resposta

a)

P X 1   +   X 2   +   X 3   ≤   200 = 0,9986

b)

P 55   ≤   X - = 0,9015

P 58   ≤ X - ≤   62 = 0,8357

c)

P X 1   +   X 2   +   X 3   ≤   160 = 0,9525

Exercícios de Livros Relacionados

Uma corrente elétrica oscilante pode ser considerada como uma variável aleatória uniformemente distribuída sobre o intervalo (9,11). Se essa corrente passar em um resistor de 2 ohms, qual será a fdp d
A resistência à compressão de amostras de cimento pode ser modelada por uma distribuição normal, com uma média de 6000 quilogramas por centímetro quadrado e um desvio-padrão de 100 quilogramas por cen
Um combustível para foguetes deve conter uma certa percentagem X de um componente especial. As especificações exigem que X esteja entre 30 e 35 por cento. O fabricante obterá um lucro líquido T sobre
Sabe-se que os erros, em certo dispositivo para medir comprimentos, são normalmente distribuídos com valor esperado zero e desvio-padrão 1 unidade. Qual é a probabilidade de que o erro na medida seja
Use a Tabela III do Apêndice para determinar as seguintes probabilidades para a variável aleatória normal padrão Z : P ( - 1Z1 ) P ( - 2Z2 ) P ( - 3Z3 ) P ( Z3 ) P ( 0Z1 )