Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Distribuição Normal

Ver Teoria
Exercício 67123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566

Enunciado

Probabilidade e Estatística – PUC-Rio – P2

Os resultados de uma pesquisa que mediu a altura dos alunos da PUC-Rio, sustentam a hipótese de que a altura de um aluno, sorteado aleatoriamente, é uma variável aleatória Normal com média 1,71m e desvio padrão 0,04m. Baseado nesta informação, responda as questões seguintes:

a) Qual é o percentil de 80% da altura dos alunos da PUC-Rio?

b) Qual a probabilidade de algum aluno selecionado ao acaso, ter altura entre 1,68m e 1,76m?

c) Se selecionarmos 12 alunos ao acaso e de maneira independente, qual é a probabilidade que a altura média deles seja superior a 1,70m?

d) Considerando a mesma amostra de 12 alunos da questão c), qual a probabilidade de que a maior altura da amostra não exceda 1,70m?

Observação:

- Mostre todos os passos da solução.

- Mostre os resultados considerando 4 casas decimais.

Passo 1

A chave para resolvermos toda esta questão é saber trabalhar com variáveis aleatórias contínuas que atendem uma distribuição normal. Em outras palavras, é saber trabalhar com aquela tabela de probabilidade de distribuição normal.

Mas qual o motivo de precisarmos utilizar aquela tabela? Vamos entender agora o quão essencial ela é.

Temos uma distribuição normal de média μ = 1,71 e desvio padrão σ = 0,04 . Então, a função de probabilidade desta distribuição é:

f x = 1 σ 2 π e - 1 2 x - μ σ 2

f x = 1 0,04 ⋅ 2 π e - 1 2 x - 1,71 0,04 2

Se queremos descobrir a probabilidade de encontrarmos uma pessoa com uma altura x na faixa de a < x < b (sejam os valores a e b pertencentes aos reais), então, “basta” calcularmos a seguinte integral:

∫ a b f x d x = ∫ a b 1 0,04 ⋅ 2 π e - 1 2 x - 1,71 0,04 2 d x

Para aqueles mais entendidos de integral, devem saber que esta integral não pode ser resolvida analiticamente. Simplesmente, não dá para resolvermos! É por isto que precisamos trabalhar com a tabela.

Passo 2

Certo, mas agora que a gente entendeu que temos que trabalhar com a tabela, como vamos encontrar o percentil de 80% da altura dos alunos da PUC-Rio, por exemplo?

Primeiro, temos que calcular um determinado valor z , que é dado pela seguinte relação:

z = x - μ σ = x - 1,71 0,04

Esta variável z é utilizada para “normalizar” o caso que estamos trabalhando. Ela possibilita com que utilizemos a tabela de probabilidade acumulada da distribuição normal.

Basta dizermos o valor de x (tipo 1,75 m) e encontraremos o valor de z , ou vice-versa. Percebam da tabela que só temos valores de z positivos x > μ = 1,71 . Isto ocorre, pois, esta função Φ z é simétrica em torno do eixo z = 0 , como pode ser vista abaixo:

Certo. Agora que a gente entendeu essa base. Como calcularemos a faixa de altura que contém 80% dos alunos?

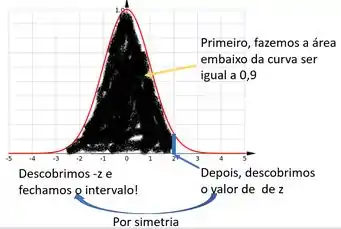
Vamos assumir que estamos trabalhando com um intervalo simétrico em torno da nossa média. Portanto, nosso intervalo é 1,71 - d < x < 1,71 + d . Logo, nosso trabalho é encontrarmos este d . Para isto, quando fizermos a comparação de x com z , através da equação que detalhamos a pouco, vamos fazer x = 1,71 + d .

Como o intervalo é simétrico, temos 40% dos alunos com altura inferior e 40% superior a média 1,71. Aqui está a dica para resolvermos o nosso problema. Basta encontrarmos o valor de z que nos dá uma probabilidade de 40% para alturas acima da média.

Utilizando a definição da probabilidade pela integração da função probabilidade, temos:

∫ - ∞ z 1 2 π e - 1 2 Z 2 d z = ∫ - ∞ 0 1 2 π e - 1 2 Z 2 d z + ∫ 0 z 1 2 π e - 1 2 Z 2 d z

Podemos rever a integral acima pelas seguintes funções probabilidades,

P - ∞ < Z ≤ z = P - ∞ < Z ≤ 0 + P 0 < Z ≤ z

P - ∞ < Z ≤ z = P - ∞ < Z ≤ 0 + 0,4

Percebam que a segunda integral do segundo membro é igual a 0,4 (40%). Continuando, temos:

Φ z = Φ 0 + 0,4

Φ z = 0,5 + 0,4 = 0,9

Temos que descobrir o valor de z então que faça com que Φ z = 0,9 . Da tabela descobrimos que é um valor entre 1,28 e 1,29 . Precisamos então fazer uma interpolação.

Interpolar nada mais é que construir uma reta utilizando os nossos dois pontos extremos. Uma equação genérica de uma reta é:

y - y 0 = Δ y Δ x x - x 0

Vamos utilizar os pontos 1,28 ; 0,8997 e 1,29 ; 0,9015 . Com isto, construímos a seguinte reta:

y - 0,8997 = 0,9015 - 0,8997 1,29 - 1,28 z - 1,28

y - 0,8997 = 0,18 z - 1,28

Agora, vamos descobrir o valor de z que nos dá y = 0,9 . Portanto,

z = y - 0,8997 0,18 + 1,28

z = 0,9 - 0,8997 0,18 + 1,28

z = 1,2817

Podemos rever todo este procedimento que fizemos e o que devemos fazer a seguir a partir da seguinte imagem:

Só que lembrem que nossa resposta não é o valor de z , temos que converter para x . Portanto,

z = x - 1,71 0,04 = 1,2817

x = 1,7613   m

Já para descobrirmos o outro extremo do intervalo, vamos utilizar o valor de - z = - 1,2817 . Portanto,

z = x - 1,71 0,04 = - 1,2817

x = 1,6587   m

Portanto, o intervalo que contém 80% dos alunos é:

1,6587 < x < 1,7613

Passo 3

Agora, vamos calcular a probabilidade de um aluno ter altura entre 1,68m e 1,76m. E ideia é bem semelhante ao que fizermos anteriormente. Vamos começar calculando o valor z para cada uma das alturas. Portanto, se z = ( x - 1,71 ) / 0,04 , então,

z 1 = 1,68 - 1,71 0,04 = - 0,75

z 2 = 1,76 - 1,71 0,04 = 1,25

Eita! Mas lá na tabela nós só temos valores de z ≥ 0 ! E agora?

Simples, basta lembrar da simetria da curva! Então, por exemplo, P - 0,75 < z < 0 = P 0 < z < 0,75 ! É sempre importante lembrarmos desta propriedade da simetria da curva.

Bom, agora vamos utilizar as propriedades da probabilidade da função normal. Com isto, poderemos utilizar a tabela para descobrirmos o valor da probabilidade de um aluno ter altura entre 1,68m e 1,76m. Portanto:

P - 0,75 < z < 1,25

P - 0,75 < z < 0 + P 0 < z < 1,25

P 0 < z < 0,75 + P 0 < z < 1,25

Para que a gente possa utilizar a tabela, precisamos começar a partir de menos infinito. Portanto, vamos fazer a seguinte transformação:

P 0 < z < c = P - ∞ < z < c - P - ∞ < z < 0

Em outras palavras, começamos a partir de menos infinito e vamos até o nosso valor final e subtraímos do intervalo de menos infinito até zero, que é igual a 0,5 (propriedades da distribuição normal após a normalização com z ). Portanto,

P - ∞ < z < 0,75 - P - ∞ < z < 0 + P - ∞ < z < 1,25 - P - ∞ < z < 0

P - ∞ < z < 0,75 - 0,5 + P - ∞ < z < 1,25 - 0,5

Da tabela, descobrimos que P - ∞ < z < 0,75 = Φ 0,75 = 0,7734 e P - ∞ < z < 1,25 = Φ 1,25 = 0,8944 . Portanto,

0,7734 - 0,5 + 0,8944 - 0,5 = 0,6678 = 66,78 %

Portanto, a probabilidade de um aluno ter altura entre 1,68m e 1,76m é 66,78%.

Passo 4

Vamos agora resolver a letra c) da nossa questão. O procedimento é semelhante ao que fizermos até agora.

Precisamos calcular a probabilidade da média de altura de 12 alunos ser maior que 1,70 m. Portanto, seria calcular a seguinte probabilidade: P x - > 1,70 .

Esse x - será a média da altura de 12 pessoas. Então, estamos tirando a média entre 12 variáveis aleatórias, o que também atenderá uma distribuição normal.

Bom, já percebemos nas outras letras que a ideia é relacionar as nossas variáveis com z (seria uma espécie de normalização dos dados). Somente após fazermos isto é que conseguiremos utilizar a tabela de probabilidade da função normal.

Portanto, a relação que iremos utilizar seria a seguinte?

z = x - - μ σ

E aí? Na verdade, precisamos fazer uma pequena alteração ao nosso z . Como a nossa média é dada por 12 variáveis aleatórias, então, seja n = 12 , o novo z será dado por:

z = x - - μ σ n = x - - 1,71 0,04 12

Portanto, a probabilidade que devemos calcular será:

P x - > 1,70

P x - - 1,71 0,04 12 > 1,70 - 1,71 0,04 12

P z > - 0,867

Só falta mais um pouco para podermos partir para a tabela de probabilidade! Vamos só utilizar as propriedades desta probabilidade como fizemos nos passos anteriores. Portanto,

P z > - 0,867 = P 0 < z < ∞ + P - 0,867 < z < 0

P z > - 0,867 = P 0 < z < ∞ + P 0 < z < 0 , 867

P z > - 0,867 = P 0 < z < ∞ + P - ∞ < z < 0,867 - P - ∞ < z < 0

P z > - 0,867 = 0,5 + P - ∞ < z < 0,867 - 0,5

P z > - 0,867 = P - ∞ < z < 0,867

Precisamos determinar P - ∞ < z < 0,867 . Para isto, vamos ter que interpolar os dados da tabela. Vamos utilizar os pontos 0,86 ; 0,8051 e 0,87 ; 0,8078 . Com isto, construímos a seguinte reta:

y - 0,8051 = 0,8078 - 0,8051 0,87 - 0,86 z - 0,86

y - 0,8051 = 0,27 z - 0,86

Agora, vamos descobrir o valor de y que nos dá z = 0,867 . Portanto,

y = 0,8051 + 0,27 0,867 - 0,86

y = 0,8070

Portanto, a probabilidade P z > - 0,867 é:

P z > - 0,867 = 0,8070 = 80,70 %

E assim finalizamos a nossa questão!

Passo 5

Agora, precisamos analisar a probabilidade de selecionar 12 alunos ao acaso e de maneiras independentes. Além disto, todos devem ter altura inferior a 1,70 m.

Então, um evento não influencia o outro. Logo, eventos independentes! Esta ideia é chave para o que vamos fazer a seguinte.

Portanto, seja p a probabilidade de encontrarmos um aluno com altura inferior a 1,70 m.

Como estamos trabalhando com eventos independentes, a probabilidade de selecionar os 12 alunos será:

p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p ⋅ p = p 12

Portanto, basta multiplicarmos a probabilidade de cada um dos eventos. Como todos possuem a mesma probabilidade, basta elevarmos ao número de alunos.

Então, nosso trabalho agora é calcularmos esse valor de p . Novamente, vamos descobrir o valor de z equivalente a x = 1,70 e vamos para a tabela. Portanto,

z = x - μ σ = 1,70 - 1,71 0,04 = - 0,25

Agora, vamos utilizar as propriedades para determinar p = P x < 1,70 = P z < - 0,25 . Vamos utilizar então o mesmo procedimento que fizemos até agora para determinar P z < - 0,25 . Portanto,

P - ∞ < z < - 0,25 = P - ∞ < z < 0 - P - 0,25 < z < 0

P - ∞ < z < - 0,25 = P - ∞ < z < 0 - P 0 < z < 0 , 25

P - ∞ < z < - 0,25 = P - ∞ < z < 0 - P - ∞ < z < 0,25 - P - ∞ < z < 0

P - ∞ < z < - 0,25 = 0,5 - P - ∞ < z < 0,25 - 0,5

Vamos na tabela para descobrir o valor de P - ∞ < z < 0,25 = Φ 0,25 . De lá, extraímos que P - ∞ < z < 0,25 = 0,5987 . Portanto,

P - ∞ < z < - 0,25 = 0,5 - 0,5987 - 0,5

P - ∞ < z < - 0,25 = 0,4013

Desta forma, obtemos que p = 0,4013 . Como queremos a probabilidade de selecionarmos 12 alunos ao acaso, temos:

p 12 = 0,4013 12 = 1,744 ⋅ 10 - 5 = 0,001744 %

Resposta

  1. O intervalo é 1,6587 < x < 1,7613 ;
  2. A probabilidade de um aluno ter altura entre 1,68m e 1,76m é 66,78%.
  3. 80,70 % ;
  4. 0,001744 %

Exercícios de Livros Relacionados

Uma corrente elétrica oscilante pode ser considerada como uma variável aleatória uniformemente distribuída sobre o intervalo (9,11). Se essa corrente passar em um resistor de 2 ohms, qual será a fdp d
A resistência à compressão de amostras de cimento pode ser modelada por uma distribuição normal, com uma média de 6000 quilogramas por centímetro quadrado e um desvio-padrão de 100 quilogramas por cen
Um combustível para foguetes deve conter uma certa percentagem X de um componente especial. As especificações exigem que X esteja entre 30 e 35 por cento. O fabricante obterá um lucro líquido T sobre
Sabe-se que os erros, em certo dispositivo para medir comprimentos, são normalmente distribuídos com valor esperado zero e desvio-padrão 1 unidade. Qual é a probabilidade de que o erro na medida seja
Use a Tabela III do Apêndice para determinar as seguintes probabilidades para a variável aleatória normal padrão Z : P ( - 1Z1 ) P ( - 2Z2 ) P ( - 3Z3 ) P ( Z3 ) P ( 0Z1 )