Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
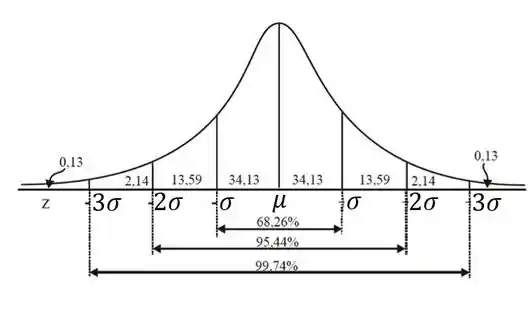
A função de densidade de probabilidade associada à distribuição normal é completamente caracterizada por sua média e seu desvio padrão . Defina o que representam estes parâmetros para a distribuição normal e esboce através de gráficos esta afirmação.
Passo 1
Aqui temos que lembrar como interpretar o gráfico da normal.
Nossa gaussiana é sempre centrada na média, ou seja, . Então o parâmetro da média define o centro da curva, o eixo de simetria do gráfico.
O desvio padrão é referente ao tamanho das caldas. Quanto maior for o desvio padrão, mais “longa” é nossa gaussiana. Ele também define as áreas onde temos , e de probabilidade ( respectivamente).
Ilustrando tudo que falamos num gráfico:
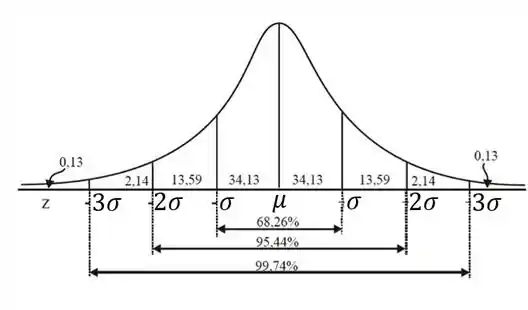
Resposta
Exercícios de Livros Relacionados
Uma corrente elétrica oscilante pode ser considerada como uma variável aleatória uniformemente distribuída sobre o intervalo (9,11). Se essa corrente passar em um resistor de 2 ohms, qual será a fdp d
A resistência à compressão de amostras de cimento pode ser modelada por uma distribuição normal, com uma média de 6000 quilogramas por centímetro quadrado e um desvio-padrão de 100 quilogramas por cen
Um combustível para foguetes deve conter uma certa percentagem X de um componente especial. As especificações exigem que X esteja entre 30 e 35 por cento. O fabricante obterá um lucro líquido T sobre
Sabe-se que os erros, em certo dispositivo para medir comprimentos, são normalmente distribuídos com valor esperado zero e desvio-padrão 1 unidade. Qual é a probabilidade de que o erro na medida seja
Use a Tabela III do Apêndice para determinar as seguintes probabilidades para a variável aleatória normal padrão Z : P ( - 1Z1 ) P ( - 2Z2 ) P ( - 3Z3 ) P ( Z3 ) P ( 0Z1 )