Tarefa da aula – 5 - Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 4
O salário semanal dos operários industriais são distribuídos normalmente em torno de uma média de R$ 180,00 com desvio padrão de R$ 25,00. Baseado nesta informação, responda as questões seguintes:
a) Encontre a probabilidade de um operário ter salário semanal situado entre R$ 150,00 e R$ 178,00.
b) Dentro de que desvios de ambos os lados da média, cairão 96% dos salários?
c) Se selecionarmos 16 operários ao acaso e de maneira independente, qual é a probabilidade que o salário médio deles seja superior a R$ 190,00?
Passo 1
a) Bom! Vamos começar dando nomes aos bois!
Pelo enunciado, a gente consegue tirar os seguintes dados...
Isso aê até agora não é novidade. Apenas o que já foi dito no enunciado!
Precisamos então, calcular a variável reduzida e recorrer a uma tabela. Então...
E o que a gente tem de fazer, é encontrar a probabilidade de um operário ter salário semanal situado entre e . Sendo assim, bora calcular duas vezes...
Para :
Para :
Passo 2
Desse modo, ficamos com...
Rearranjando...
Rearranjando de novo! Podemos escrever a expressão acima como...
Sendo assim;
E então, dando uma olhada na tabela abaixo...
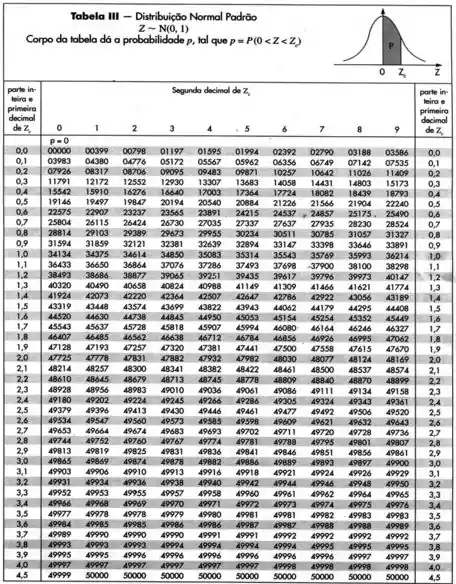
Obtemos o seguinte resultado...
Passo 3
b) Nesse segundo item aqui, precisamos dos desvios onde cairão 96% dos salários...
Ou seja, o que a gente quer é que aconteça o seguinte...
Ou no caso, como a nossa tabela só vai até ...
Dando uma olhada na tabela, a gente tem que . Sendo assim...
Como a tabela só vai até metade, e precisamos do outro extremo de , é só pegar o negativo ...
Ficamos então, com...
Passo 4
c) Hummm! Agora temos o caso de uma distribuição por média!
Como a gente viu, a média tem distribuição normal assim:
Então, nesse caso teremos que...
Calculando o que foi pedido, isto é...
Padronizando...
Dando uma olhada na tabela, tomando cuidado com o fato de que ela só vai até , ou seja, teremos que multiplicar por a probabilidade em no final das contas e dividir por dois, depois que subtrair de ...
Resposta
a)
b)
c)