Você chega ao check-in de um aeroporto carregando uma mala que contém 10 pacotes de café, 5 pacotes de tapioca e 7 pacotes de feijão. Suponha que os pesos desses itens são todos variáveis aleatórias independentes com distribuição normal com as seguintes médias e desvios-padrão:
Pacote de café: média e desvio-padrão .
Pacote de tapioca: média e desvio-padrão .
Pacote de feijão: média e desvio-padrão .
Suponha que o peso da mala vazia é , e que, além disso, você ainda carrega exatos de roupas. Pede-se:
a) Determinar o valor esperado e a variância do peso total da bagagem detalhando todos os cálculos. Qual a probabilidade de que o peso de sua bagagem exceda os permitidos para o embarque?
b) No counter foram amostradas 25 bagagens com um peso médio de e desvio-padrão de . A aviação aérea deseja saber qual a probabilidade de que o peso médio das bagagens esteja entre e kg.
c) Considere como sendo a média e a variância do peso total da bagagem aquelas fornecidas no item (b). Para um tamanho de amostra , qual a probabilidade da mala com menor peso exceder ?
Passo 1
Fala pessoal, beleza? Prontos para mais uma questão de probabilidade?
O peso da bagagem será o peso da mala vazia junto com de roupa e os pacotes de café, tapioca e feijão. Portanto, o peso total será dado por
Para achar o peso dos pacotes de café, temos que escrever
Tomando o valor esperado, temos que
Mas como , temos que
Analogamente, temos
Logo,
Substituindo as médias em :
Com isso vemos que o valor esperado do peso total da bagagem é . Para achar a variância, fazemos algo parecido:
Como todas as variâncias são iguais a :
Analogamente,
Com isso, temos que
Como , temos que
Passo 2
Depois de todas as contas que fizemos no passo 1, vemos que o peso total da bagagem é uma variável aleatória com valor esperado e variância . Como se trata de uma soma de variáveis que seguem uma distribuição normal, a distribuição dela também será normal!
Lembre-se que tudo que precisamos para uma distribuição normal é sua média e sua variância e, nesse caso, já temos as duas 😊.
Queremos saber qual a probabilidade de . Para isso, fazemos a tradicional mudança de variável:
Com essa transformação, nós achamos uma distribuição normal de média zero e desvio-padrão um para a variável . Essas são as distribuições que temos em tabelas.
Para que , temos que
Logo,
Com isso, queremos achar:
Geralmente as tabelas têm as probabilidades para até mais ou menos, pois acima disso as probabilidades são muito muito muito muito pequenininhas. Desta forma, podemos praticamente escrever:
Portanto, podemos dizer que a probabilidade de o peso da bagagem ser maior que é tão pequena, mas tão pequena, que é praticamente nula!
Passo 3
Partiu item (b)?
Bom, agora o enunciado falou para gente que pegaram uma amostra com bagagens e média e desvio-padrão amostral foram:
Primeiro temos que achar o desvio padrão da média:
Daí, definimos a transformação de variável:
Queremos saber a probabilidade de o peso médio estar entre e , ou seja,
Usando , achamos
Já para :
Com isso, queremos saber:
Portanto,
Como discutido no passo 3, para maior que 4 a probabilidade vai ser tornando cada vez menor. Assim, a probabilidade de estar entre menos infinito e é praticamente . Logo, podemos escrever:
Passo 4
Para achar , recorremos à tabela:
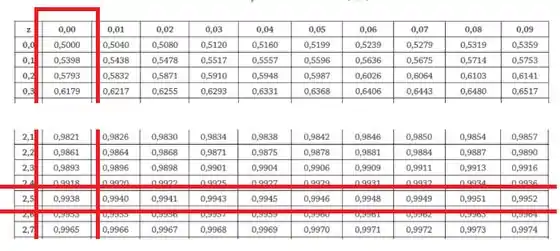
Vemos que
Portanto,
Passo 5
Estamos quase acabando, falta só o item (c)...
No item (b) nós dividimos o desvio-padrão pela raiz de para obter o desvio-padrão da média já que o problema queria estudar a distribuição da média. Aqui no item (c) nós não devemos fazer isso pois agora ele quer analisar a distribuição individual de uma das bagagens da amostra. Portanto, vamos usar
Com isso, a variável fica
Queremos saber a probabilidade de . Substituindo na relação para :
Portanto, queremos:
Olhando na tabela:
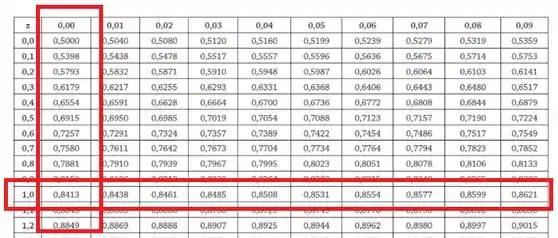
Logo,
Logo,
Aqui fechamos a questão 😉.