05) Uma fábrica produz parafusos com resistência ao torque , a qual deveria ser no mínimo . Assuma distribuição normal para a resistência. Verificou-se que com a regulagem atual do processo dos parafusos saem com resistência menor que . O engenheiro do processo aumentou a resistência média em para tentar resolver o problema (mantendo a variância). Agora dos parafusos ainda caem abaixo de . De quanto deve ser aumentada novamente a resistência média (mantendo a variância) para que apenas dos parafusos caíam abaixo de ?
A)
B)
C)
D)
E)
Passo 1
Eaí pessoal, tudo certinho com vocês?
Nessa questão, temos uma fábrica de parafusos, cuja resistência segue a distribuição normal. O objetivo do processo de fabricação, é maximizar a quantidade de parafusos que saem com resistência maior do que . Para isso, o engenheiro tenta mexer na resistência média, sem alterar a variância, pra conseguir diminuir a porcentagem de parafusos com baixa resistência.
O nosso objetivo é calcular em quanto que devemos aumentar a resistência média de modo que apenas dos parafusos tenham menos do que de resistência.

Mas vocês lembram do que se trata a distribuição normal?
Falando bem o basicão, a gente precisa lembrar que ela tem um gráfico na forma de sino, e que pra calcular as probabilidades dessa distribuição costumamos normalizar a V.A para consultar uma tabelinha já pronta. É só fazer:
E consultar a tabelinha (que de pequena não tem nada), que vai ter essa cara daqui:
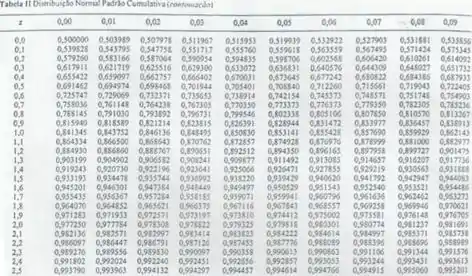
Massa! Agora bora voltar pra questão!
Passo 2
Beleza, já não estamos mais perdidos no exercício, mas o que devemos fazer agora?

Então, o objetivo é descobrir o quanto que vamos aumentar a resistência média de modo que a probabilidade de termos um parafuso delituoso seja de . Matematicamente falando, queremos que:
Normalizando a probabilidade, temos:
Daí, escrevendo a probabilidade normalizada, vem:
Consultando a tabelinha, vemos que o valor de que dá uma probabilidade de , vale:
Logo, queremos ter:
Logo:
Passo 3
Beleza, estamos quase lá! Precisamos calcular o desvio padrão e também a resistência média antiga.
Para isso, vamos usar duas informações que temos pelo enunciado:
1) Inicialmente, com a regulagem utilizada, a probabilidade de ter um parafuso defeituoso era de . Ou seja:
Novamente, pela tabelinha, temos:
2) Após aumentar a resistência média em , a nova probabilidade vale . Logo:
Pela tabelinha, ficamos com:
Beleza, fazendo , temos:
Logo:
Mas, como sabemos a relação entre a nova resistência média e o desvio padrão, podemos escrever que:
Portanto:
Assim, o aumento em relação à última resistência média atualizada pelo engenheiro (, vale:
Por fim, finalmente temos que a resistência média deve ser aumentada em:
Prontinho gente! Espero que vocês tenham entendido direitinho, até a próxima 😉
Resposta
Letra C: