Calcular a área delimitada por e .
A intersecção será correspondente a e a área
A intersecção será correspondente a e a área
A intersecção será correspondente a e a área
A intersecção será correspondente a e área
Passo 1
Eaew, belezinha?
Nós precisamos calcular a área entre duas curvas, sendo elas, e , as alternativas dão informações sobre as intersecções entre as curvas, o que será necessário para calcularmos os limites de integração durante o problema, assim como dá a resposta em (unidades de área). Vamos começar visualizando a nossa região, ela é da seguinte forma
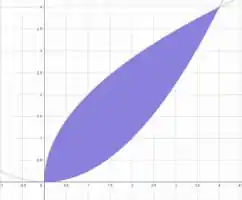
Para o plot da região utilizei , portanto, ignore os valores nos gráficos, belezinha? A área de uma região pode ser obtida calculando a área sob a curva de cima, e então, subtrair a área da curva de baixo, isso pode ser obtido resolvendo a seguinte integração
Vamos utilizar isso para resolver a nossa questão!
Passo 2
Primeiro precisamos encontrar quem são os nossos limites de integração. Assim como a figura indica, isso acontece em dois pontos onde as curvas se interceptam! A intersecção pode ser obtida fazendo
Em que temos e . Portanto, temos
Podemos obter como
Observando o gráfico, esta é a intersecção final, a inicial é obtida em , único outro ponto onde a igualdade das funções é mantida. Vamos então escrever a nossa integral!
Passo 3
Temos a seguinte integral para a área
Vamos resolver uma integral de cada vez!
Passo 4
Vamos resolver primeiro
Ela pode ser reescrita da seguinte maneira
Resolvendo os últimos detalhes e expandindo os índices, temos
Que pode ser escrito como
A primeira integral foi isso! Vamos resolver a outra!
Passo 5
Temos
Identificando a nossa primitiva como
Avaliando os limites, temos
Só falta juntar tudo agora! Vamos lá!
Passo 6
Finalmente, temos a nossa área como
Somando ambos os termos
Portanto, como nossa intersecção ocorreu em e a área é . A única alternativa verdadeira é a . A questão foi isso, te vejo na próxima! Tchau Tchau!