UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV1 - 2022.1, Questão 4
Seja o campo vetorial dado por :
O campo vetorial é conservativo? Caso seja positivo, encontre a função potencial tal que ;
Calcule o trabalho realizado pelo campo de força acima, ao mover um objeto ao longo da curva dada pela função , .
Passo 1
Oiiie, tudo bem?
A questão nos dá um campo vetorial
a primeira alternativa pede para que verifiquemos se é um campo conservativo, ou não. No caso do mesmo ser, é preciso encontrar uma função potencial . Para que um campo seja conservativo esta função deve existir, e além disso, é necessário que
ou seja, o campo vetorial deve ter rotacional nulo! Iremos usar ambas estas necessidades para resolver a primeira alternativa! Se, o campo for conservativo, isso nos ajudará na segunda alternativa que pede para calcularmos o trabalho de uma força dada pelo campo vetorial ao longo da curva
,
Isso é uma vantagem, pois se for conservativo, o trabalho pode ser calculado através do teorema fundamental da integral de linha como
em que e são os pontos iniciais e finais, relativos ao início da curva em e o final em . Vamos tentar fazer isso! Vem comigo!
Passo 2
Primeiro, vamos verificar se o rotacional do campo vetorial é nulo, temos que
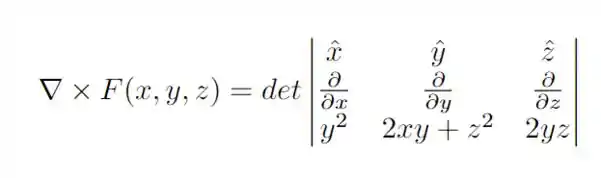
Calculando o determinante, obtemos a seguinte relação
Lembrando que quando estamos derivando parcialmente, consideramos todas as outras variáveis que não estão sendo derivadas como constantes, portanto, podemos escrever as derivadas acima, da seguinte forma
O rotacional é nulo, portanto o primeiro passo para o nosso campo ser conservativo é válido! Nas derivadas acima foi necessário usar basicamente a regra do tombo para polinômios! Vamos procurar agora uma função potencial!
Passo 3
O enunciado nos dá a condição para que uma função seja uma função potencial, temos que
No lado esquerdo, temos o gradiente do potencial, lembrando que o gradiente é tal que
De forma que obtemos três equações para a função potencial, lembrando que nosso campo vetorial é
podemos escrever as três equações como
e, também que
e, por último
Com estas três equações deve ser possível identificar quem será nossa função potencial! Vamos lá!
Passo 4
Vamos integrar “parcialmente” cada uma das equações acima, primeiro integrando em relação a a primeira equação, temos que
Note que ao integrar parcialmente em uma variável, nós não deixamos em aberto uma constante arbitrária, e sim uma função arbitrária nas outras duas variáveis! Agora, integrando parcialmente a segunda equação em , temos que
e, por último, integrando parcialmente em , temos
Será que é possível identificar quem são estas três funções? SIM! Se olharmos as três em conjunto, podemos encontrar termos em comum, e termos que se complementam. Por exemplo se tomarmos que , e que . Podemos escrever que nossa função potencial é simplesmente
Maravilha! Essa é a nossa alternativa Vamos para a segunda agora!
Passo 5
Como vimos que o nosso campo vetorial é conservativo, podemos calcular o trabalho pedido pelo teorema da integral de linha, ou seja
Ainda precisamos saber quais são as coordenadas iniciais e finais no entanto. Isso é bastante direto já que nos foi dada a curva na forma
em , nós obtemos que
da mesma forma, temos para , que
Ou seja, nosso trabalho é dado por
Vamos usar a função potencial e terminar com essa questão! Bora lá!
Passo 6
Podemos calcular que
e, também que
Finalmente, o trabalho realizado por este campo vetorial ao longo da curva, é
A questão é isso! Te vejo na próxima! Tchau Tchau!
Resposta
O campo é conservativo com e o trabalho realizado é .