IME, Cálculo 1, 2019, VE2, Q4
Seja , definida abaixo:
- Determine se é inversível em seu domínio.
- Determine quantas raízes possui.
Passo 1
Faaaala, molecada! Repara que se supormos que a função não seja injetora, temos que existem , tais que:
E daí, pelo Teorema de Rolle, como é contínua e diferenciável, temos que existe tal que:
Contudo, aplicando o Teorema Fundamental do Cálculo na função, temos:
Contudo, observe que
Logo, segundo o círculo trigonométrico abaixo, observe que esses senos como argumento de cossenos, fazem-nos tomarem valores positivos.
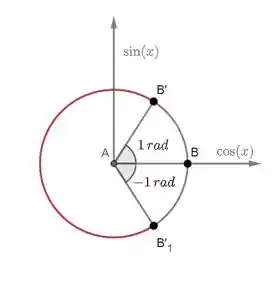
Assim,
Tal que para , domínio de , temos:
Desta contradição, temos que tem de ser injetora. Assim, se definirmos , temos bijetora e, portanto, inversível.
Passo 2
Para respondermos a letra é sempre valioso relembrarmos que funções integrais são nulas quando seus limites se igualam. No caso de:
Isto ocorre para:
Para , , logo: . Como é injetora, essa deve ser a única raiz de .
Resposta
- é inversível.
- Apenas é raiz.