Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais.
Passo 1
O problema nos pede para usarmos as propriedades das integrais e aparece uma desigualdade. Queremos provar que a integral está entre e sem calculá-la.
Passo 2
Temos uma integral e uma desigualdade. Isso tem uma carinha de que devemos usar aquelas propriedades de integrais definidas que envolvem desigualdades.
A função trata-se de um polinômio, e todo polinômio é uma função continua. Deste modo, em um intervalo fechado vamos ter um mínimo, , e um máximo, .
Através dos limites de integração, sabemos qual é o intervalo fechado ( . E a função é contínua nesse intervalo.
Nesse caso, vamos pensar na seguinte propriedade:
Para podermos usá-la a nosso favor, entretanto, devemos achar o mínimo e o máximo absolutos de no intervalo .
Que tal desenharmos o gráfico dessa função para visualizar melhor?
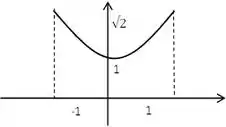
Pelo gráfico da função nesse intervalo, identificamos o mínimo e o máximo local:
Podemos utilizar, então, a propriedade:
Conforme queríamos demonstrar!
Resposta
Ei, a resposta está no passo a passo :)