UFPE – Cálculo 1 – Lista 7 – Professor Matheus Nunes
3. Extras
a) Para a função dada abaixo, esboce seu gráfico e em seguida calcule
Passo 1
Faaalla... tudo bem??
Nessa questão vamos fazer o gráfico da função e calcular a integral .
Repara que temos uma função definida por partes (ela tem um comportamento diferente pra cada intervalo dado). Então, pra calcular a integral, dividimos em integrais conforme os intervalos estão divididos:
Mas bora pra questão pra ficar mais fácil de enxergar...
Passo 2
Primeiro fazendo o gráfico dessa função definida por partes:
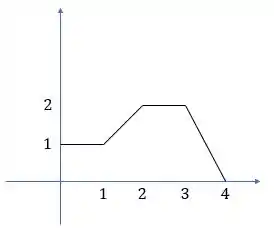
Passo 3
E pra calcular a integral:
Substituindo pela definição de cada intervalo da função:
Resolvendo:
Resposta
Exercícios de Livros Relacionados
Use um sistema de computação algébrica para calcular a integral. Compare a resposta com o resultado usando as tabelas. Se as respostas forem diferentes, mostre que elas são equivalentes. ∫ x 2 1 - x 2
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit
Uma partícula move-se com aceleração a tm / s 2 ao longo de um eixo s e tem velocidade v 0m / s no instante t = 0 . Encontre o deslocamento e a distância percorrida por ela durante os intervalos de te
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit