USP – Sem Campus – Cálculo 1 – Provas Antigas – P2 IME -2021.1 - 6
Sejam e A área da região limitada pelos gráficos de e e pelas retas e é igual a:
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Para calcular essa área da função, precisamos primeiro saber como esses gráficos se comportam dentro do gráfico. Temos então:
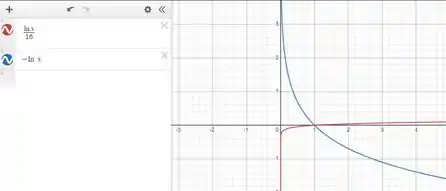
Sendo a área, a soma das áreas indicadas nas setas:
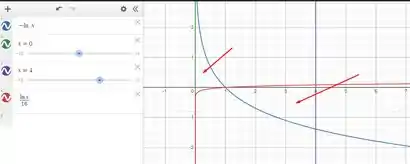
E agora precisamos achar esse ponto de intersecção. Tudo bem que pelo gráfico é fácil de achar que é 1, mas calculando isso sem a ajudinha do gráfico, temos:
Isolando,
Sendo a única solução real.
Passo 2
Passo 3
Outro ponto bastante importante a se observar antes de calcular a área é que antes do ponto , a função está “acima” da função . E após esse ponto, que está “acima” de . Isso é suuuper importante, pois vai nos ditar como vamos montar a nossa integral. Dentro dos intervalos de integração, quem está por cima vem primeiro na subtração. Segue o modelo. Primeiro calculando essa área:
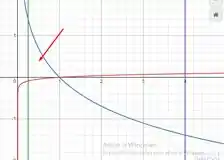
Nela, está acima. Logo a integral vai ficar no formato:
Analogamente, para a segunda área,
E portanto, a área total vai ser a soma das duas áreas:
Passo 4
Agora bora resolver as integrais e achar a resposta da questão! Resolvendo:
Resposta
b)