UnB; Cálculo 1; Lista 15; Exercício 4f
4) Calcule cada uma das integrais abaixo.
(f)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!
Vamos lá, pessoal! Pra resolvermos esse exercício aqui, primeiro precisamos definir que método utilizaremos! Tá, mas como eu faço isso?
Nesse caso específico aqui, antes de qualquer coisa, vamos observar que temos um polinômio dividindo outro! Isso aqui vai nos ajudar bastante pois quando fizermos essa divisão, provavelmente chegaremos em uma expressão bem mais simples!
Bora lá fazer essa divisão então!
Temos do enunciado que:
Então, vamos dividi-lo como faríamos uma divisão comum:
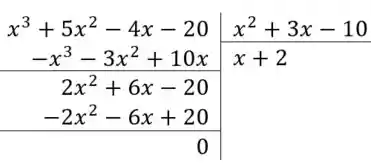
Olha só que legal!! Aquela expressão feiona de divisão pode simplesmente ser substituída pelo resultado da divisão feita aqui em cima!! Uhul!!
Então a nova integral a ser calculada é:
Bora lá resolver isso aí então!!
Passo 2
Como na integral do passo acima temos uma soma, podemos fazer o seguinte:
Resolvendo cada uma das integrais acima temos que:
Lembrando aqui que é a nossa constante de integração!!
Simplificando o nosso resultado vamos ter que:
Conseguimos!!!! Doce como o mel!
Pra essa questão é isso pessoal! Bora pra mais uma?