UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Prof° Ricardo Martins - Listas sobre Integrais, Questão 8.10
Determine se converge ou diverge, se convergir, determine seu valor.
Passo 1
Eaew, belezinha?
Temos que determinar se a seguinte integral é convergente
ou seja, avaliar se ela resulta em um valor finito após avaliarmos a integração. Para esse caso não precisamos nem sequer integrar! Vamos analisar o nosso integrando!
Passo 2
Note o que acontece quando tomamos o seguinte limite
da mesma forma, temos que
Como a nossa integração passa por , necessariamente a área (resultado da integração) irá divergir, note o gráfico de nosso integrando
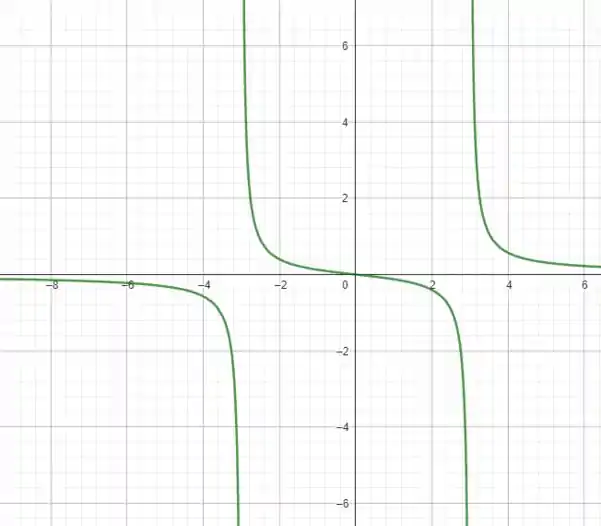
Sendo assim, a integral imprópria é divergente! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
A integral é divergente!
Exercícios de Livros Relacionados
Use um sistema de computação algébrica para calcular a integral. Compare a resposta com o resultado usando as tabelas. Se as respostas forem diferentes, mostre que elas são equivalentes. ∫ x 2 1 - x 2
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit
Uma partícula move-se com aceleração a tm / s 2 ao longo de um eixo s e tem velocidade v 0m / s no instante t = 0 . Encontre o deslocamento e a distância percorrida por ela durante os intervalos de te
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit