![]()
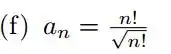
Passo 1
Bora começar fazendo o teste da divergência? Lembra dele?
Relaxa, não é nada mais que calcular o limite do termo geral quando . Se esse limite der diferente de zero, a série diverge, e se for igual a zero, nada podemos concluir (temos que fazer outro teste).
Eu sei, eu sei... Eu sei que envolve fatorial, mas veja bem, esse exemplo vai ser bem tranquilo de calcular:
Aeeeee! A nossa série diverge!
Atenção!!! Normalmente, quando o termo envolve fatorial, não é recomendado fazer o teste da divergência, pois fica muito complicado fazer o limite. Porém, nesse caso foi molezinha.
Resposta
A série diverge.