Seja
- A derivada de é dada por:
- A função é, para :
- Em relação à série é correto afirmar que
- A série converge pelo teste da integral
- A série diverge pois
- A série diverge pelo teste da integral
- O teste da integral nãos e aplica por que é crescente
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar você!
A questão começa dando uma função :
- na letra (a) pede apenas a derivada dela: aqui não tem mistério, é lembrar de todas as regrinhas de derivação lá do cálculo 1!
- Na letra (b) ele pediu para dizer se a função é crescente ou decrescente em . Isso está relacionado com a derivada! Se a derivada nesse ponto (em diante) for negativa, quer dizer que a função é decrescente, se a derivada for positiva, significa que a função é crescente. Tranquilo?
- Na letra (c) o problema pergunta várias coisas acerca da série que está associada com a função dada. Ele fala no teste da integral, então não custa nada rever como ele funciona:

Se concluirmos que a função é decrescente (e isso vamos fazer isso no item (b)), no item (c) precisamos aplicar esse teste. A ideia é integrar essa função e analisar o resultado. Se for um resultado finito, significa que a integral converge e assim a série também converge. Se o resultado for , significa que a integral diverge, assim como a série.

Mas calma, vou fazer essa questão junto com você!
Bora lá?
Passo 2
Letra (a) - a função é:
Sua derivada:
Tranquilo? Aqui é só fazer isso mesmo!
Passo 3
Letra (b) – agora vamos analisar o sinal da derivada para ver se a função é crescente ou não!
Aplicando em :
Como o denominador é sempre positivo, quem “manda” no sinal é o numerador. Como temos um sinal de na frente de tudo, essa derivada é sempre negativa para positivo! O importante é que depois desse ponto (), ela seja sempre decrescente, e é isso exatamente que acontece aqui!
Então podemos dizer que essa função é decrescente para !
Passo 4
Letra (c) – agora vamos aplicar o teste!
Agora vamos partir para a integral!
Agora vamos calcular a integral dessa função de até :
É uma integral imprópria, e o truque sujo é o seguinte: chama aquele de uma letra qualquer, por exemplo “b”, e põe por fora dessa integral um limite de . Isso vai fazer com que você consiga calcular a integral sossegado e depois avaliar o limite no infinito, beleza?
 aplicando esse truquezinho temos o seguinte:
aplicando esse truquezinho temos o seguinte:
Vamos resolver essa integral separadamente!
Passo 5
A integral dentro do limite é:
#AVISOTRUQUESUJO
No denominador, vou escrever dessa forma aqui:
Mas por quê? Por que assim consigo ter algo do tipo:
E essa integral é tabelada! Relembrar é viver... então
Beleza até aqui?
Voltando ao denominador:
Escrevendo em termos de produto notável e temos:
E aí nossa fração fica assim
E comparando com o que tínhamos
Com , e . Assim nossa integral é:

Vamos voltar ao nosso limite?
Passo 6
Queríamos avaliar esse limite aqui:
E resolvemos separadamente a integral, pegando o resultado que achamos no passo anterior e substituindo ali dentro do limite temos o seguinte:
Acontece que a função arco tangente tente à no infinito!
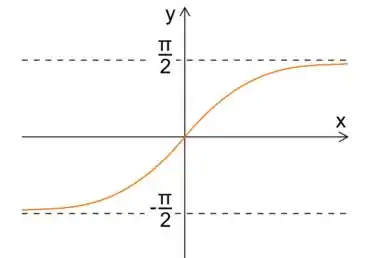
Sendo assim
Que é finito!

Então, se
Então a série
Recapitulando as alternativas da letra (c):

Marcamos apenas a primeira alternativa!
Tranquilo? Espero ter ajudado!
Até a próxima!
Resposta
A série converge pelo teste da integral