Energia Potencial e Conservação da Energia Mecânica
1b) Na figura, um bloco de cai a partir do repouso de uma altura , e desliza num plano inclinado e numa pista sem atrito até bater numa mola relaxada . Na região onde a mola se encontra, existe atrito cinético entre o bloco e o solo . Nestas condições, calcule a compressão máxima da mola.
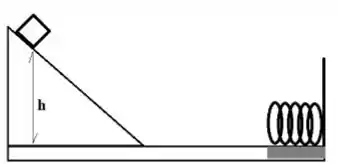
Passo 1
Sabemos pelo teorema trabalho-energia que:
Entretanto, na compressão máxima da bola, a velocidade do bloco é nula. Logo, e ficaremos com:
A energia cinética inicial do bloco, no momento anterior a chegar na mola, pode ser encontrada por conservação de energia mecânica, ela é justamente a energia potencial no inicio do movimento. Assim:
Então, substituindo:
Por outro lado, temos também:
Onde:
Durante a compressão e (sendo ). Assim, temos:
Re-escrevendo esta equação, dividindo tudo por e multiplicando por 2, para deixar o termo ao quadrado isolado:
Resolvendo a esquação do segundo grau, teremos:
Substituindo os dados do enunciado:
Tomando apenas a raiz positiva:
Assim, a compressão máxima é .