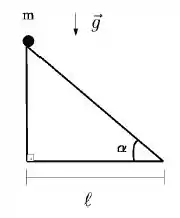
Um corpo de massa desliza do topo de uma rampa cuja base tem comprimento , conforme a figura abaixo. O coeficiente de atrito dinâmico entre o corpo e a superfície da rampa é . Qual deverá ser a relação satisfeita pelo ângulo () para que o tempo de deslizamento do corpo ao longo de toda rampa seja o maior possível?
Obs: Mínimos e máximos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.
(a)
(b)
(c)
(d)
(e)
Passo 1
A questão é sobre uma partícula descendo um plano inclinado e sofrendo uma força de atrito cinética .
O que acontece num plano inclinado é que a componente das forças (na direção da rampa e perpendicular a ela) atuando sobre a partícula dependem da inclinação da rampa .
Então, conforme variamos essa inclinação, isso vai causar um efeito sobre o movimento dela.
Mas vem cá, nosso objetivo é o maior tempo possível para que ela desça a rampa, certo?
Certo!
Então é só a gente diminuir a inclinação da rampa até que essa partícula desça com as menores aceleração e velocidade possíveis, certo??
NÃOOOO!

Então... existe uma pegadinha nessa questão que é a seguinte:
O que é fixo da rampa é o comprimento da base :
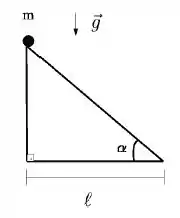
Ou seja, conforme aumentamos a inclinação da rampa, a distância que a partícula percorre (comprimento da hipotenusa) aumenta também.
Assim, temos que realmente achar uma expressão para o tempo que a partícula leva em função desses parâmetros e maximizar isso usando a dica da questão:
Obs: Mínimos e máximos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.
Passo 2
Vamos começar fazendo o diagrama de forças sobre a partícula:
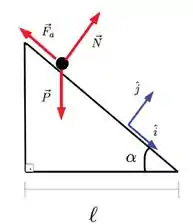
Podemos ainda decompor a força peso nas suas componentes paralela e perpendicular à rampa:
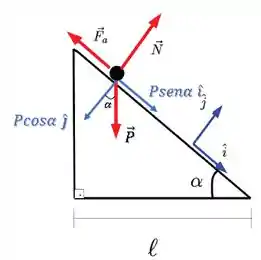
Mas como chegamos no tempo a partir dessas forças??
A partir das forças conseguimos a aceleração (Segunda Lei de Newton).
A partir da aceleração e o deslocamento, conseguimos o tempo .
Passo 3
Vamos aplicar a Segunda Lei de Newton na direção da rampa:
A força peso é dada por , enquanto a força de atrito , por ser cinética, é dada pelo coeficiente de atrito cinético vezes a força normal :
Mas podemos encontrar essa força normal fazendo o equilíbrio na outra direção:
Substituindo isso na outra expressão, achamos uma expressão para a aceleração:
Passo 4
Agora, precisamos escrever a distância percorrida pela partícula (hipotenusa) em função dos parâmetros:
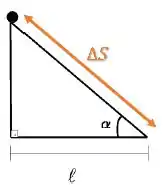
Podemos relacionar isso com:
Passo 5
Já temos a aceleração e o deslocamento . Vamos encontrar o tempo .
Como a aceleração da bolinha é constante ao longo de todo o trajeto, realiza um movimento uniformemente variado:
Vamos considerar a origem no seu ponto de partida e o movimento ao longo da direç��o da rampa (eixo ), além disso, vamos considerar sua velocidade inicial sendo nula, então:
Substituindo:
Pronto, agora só precisamos maximizar .

Passo 6
Para que tenha um valor máximo:
O que está dentro da raiz quadrada deve ter valor máximo, certo?
Certo!
E para que esta fração tenha valor máximo, o denominador deve ter valor mínimo, certo?
Certo!
Então, vamos minimizar essa expressão, que chamaremos de .
Passo 7
Para minimizar, vamos derivar e depois igualar a zero.
Aplicando a regra do produto, temos:
Multiplicando os parênteses:
Somando os termos em comum:
Colocando em evidência:
Passo 8
Antes de igualar a zero, podemos usar duas identidades trigonométricas para melhorar a cara da nossa expressão.
A primeira vem a partir do “Minha terra tem palmeiras onde canta o sabia, .
Hahah, enfim, alguns aprenderam decorando essa musiquinha:
Mas se os ângulos forem iguais a , temos:
Esse termo aparece lá no meio da nossa expressão...
A segunda relaç��o é do cosseno da soma de ângulos:
E se os ângulos forem iguai a , temos:
Essa relação também aparece na nossa expressão.
Passo 9
Usando isso em :
Passo 10
Agora, basta igualar isso a zero:
Se o produto de com o termo em parêntesis deve dar zero, temos que:
Podemos dividir tudo por , já malandramente olhando para aquele “” das alternativas:
E assim achamos finalmente a nossa resposta!

Resposta
Letra (d)