USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e e Energia, Questão 46
Um cubinho de gelo escorrega sobre um plano inclinado de inclinação no dobro do tempo que leva para escorregar em um plano análogo, mas sem atrito. Qual é o valor do coeficiente de atrito cinético entre o gelo e o plano?
Passo 1
Eaew, tudo bem com você?
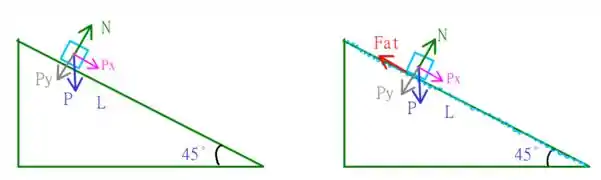
O esquema acima indica a situação indicada no enunciado. Note que no caso da esquerda o cubo de gelo leva o dobro de tempo para percorrer o caminho de comprimento do que no caso da direita (que tem atrito). Temos tempo e deslocamento envolvidos, portanto, é uma dica para que usemos a equação horária do movimento, que diz que
A questão é, que para um deslocamento , temos que , ou seja, a situação do lado esquerdo leva duas vezes mais tempo que a situação no lado direito! Porquê? Vamos descobrir!
Passo 2
O que ocorre é que no caso do lado esquerdo temos nossa aceleração causada unicamente pela componente do peso dada por
de forma que nossa aceleração é
No caso da direita, temos que o atrito gera um termo que atenua a aceleração for um fator constante, já que
Como temos que a normal é equivalente a componente perpendicular ao plano do peso, temos que
sendo assim, temos que a aceleração no segundo caso é dada por
Maravilha! Vamos usar agora a equação horária do movimento para ambas as equações!
Passo 3
Temos que o deslocamento é o mesmo para os dois casos, portanto, temos que
em que estou considerando ambos partindo do repouso! Substituindo as acelerações obtidas, e simplificando, temos que
Mas lembre que , portanto, essa expressão se torna
Simplificando em ambos os lados temos que
ou seja, isolando o coeficiente, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!