UFABC – Fenômenos Mecânicos – Lista 3 – Questão 11
Um bloco de massa está apoiado sobre o lado esquerdo de um bloco de massa . O coeficiente de atrito cinético entre os dois blocos é de 0,3 e a superfície sobre a qual o bloco de está apoiado é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento como mostrado na figura abaixo. Se a distância que a superfície frontal do bloco menor percorre sobre o bloco maior é de .
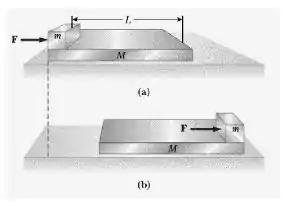
a) Quanto tempo levará até esse bloco chegar ao lado direito do bloco de , como mostrado na figura? (Observe: os dois blocos são colocados em movimento quando é aplicada.)
b) Qual a distância percorrida pelo bloco de nesse processo?
Passo 1
Oi pessoal, tudo bem? Primeiro vamos fazer um desenho para ver quais forças estão agindo nessa situação:
Ao longo do eixo horizontal agem a força e a força de atrito , que são responsáveis pela aceleração
Tranquilo até aqui?
No bloco maior de massa M, agem também a normal (da mesa e do outro bloco, representadas como e ) e o peso (Mg).
O problema pede para calcularmos o tempo que o bloco menos leva para chegar até o outro lado e qual é a distância percorrida. Bom, para isso precisamos antes calcular a aceleração! Ela é quem vai nos dizer como o movimento vai ser!
Depois de calculada a aceleração podemos encontrar o tempo de travessia! E com esse tempo, podemos encontrar a distância percorrida pelo bloco de baixo!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A aceleração do bloco menor pode ser calculada usando a segunda lei de Newton, ou seja:
Tranquilo?
Lembrando que e que, nesse caso,
Essa é a aceleração com que o bloco menor se movimenta! Beleza?
Da mesma forma, aplicando a segunda lei de Newton para o bloco maior, temos que:
Com as acelerações, podemos montar a equação da posição em função do tempo dos blocos!
Passo 3
Vamos escrever a equação de movimento para os dois blocos:
Bloco menor:
Bloco maior:
O que elas têm em comum? O tempo! Ao mesmo tempo que o bloco de cima percorre a distância , o de baixo percorre . Então antes de tudo vamos encontrar a letra (b)!
Dividindo uma equação pela outra obtemos:
Lembrando que e temos
Essa é a distância que o bloco de massa M anda! Então encontramos a letra (b) no meio do percurso, mas não tem problema! já guarda esse resultado!
Passo 4
Agora queremos saber o tempo que o bloco leva para atravessar. Como já achamos o valor de , podemos substituir ele na segunda equação (equação da posição para o bloco maior):
Sendo assim o tempo é (letra (a)) e a distância é . E é isso!
Espero ter ajudado!