UNICAMP – Física 1 – 2019.1 – Exame – M.Escolha
1. Um carro de massa sobe uma rampa que faz uma inclinação de com a
horizontal a uma velocidade de 20 m/s. Ao acionar subitamente os freios, passa a derrapar,
percorrendo uma distância de metros até parar. A força de atrito entre os pneus e o chão
vale:
zero
Passo 1
Vem comigo para a gente resolver esse problema juntos!
Ele está pedindo a força de atrito. Para achá-la teremos que usar a segunda lei de Newton e analisar a força resultante na horizontal, já que ele não nos deu coeficiente de atrito.
Ele diz que depois dos freios acionados o carro percorre até parar, mas que isso aconteça temos que ter uma força resultante atuando sobre o carro até ele parar.
Mas quais forças compõem essa força resultante? Vamos montar um diagrama de corpo livre do carro, temos:
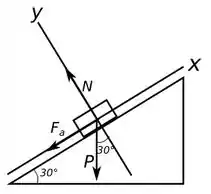
A força de atrito só atua na direção então temos que usar a segunda lei de Newton nessa direção. Se você reparar, além da força de atrito temos a força peso contribuindo na direção também. Com isso poderemos encontrar .
Vamos lá então!
Passo 2
A segunda lei de Newton para direção é dada por:
Isolando , temos:
Mas para continuarmos precisamos saber quem é .
Passo 3
Então pensa aqui comigo, a força resultante é a responsável por parar o carro, então essa aceleração é a aceleração que faz o carro parar.
Então teremos que usar nossos conhecimentos de cinemática para achar essa aceleração. Como temos a velocidade inicial e final e o deslocamento do carro até parar podemos usar a seguinte equação:
Substituindo com os valores que temos, ficamos com:
Então temos que:
Passo 4
Agora podemos encontrar a força de atrito , temos:
Substituindo os valores conhecidos, temos:
Então temos que:
Logo a opção correta é a letra .