Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito Cinético

Ver Teoria
Exercício 25123456789101112131415161718192021222324262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576

Enunciado

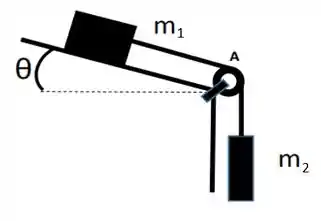
Parte I - Considere a figura mostrada nessa questão e forneça suas respostas em notação científica no sistema internacional de unidades considerando rigorosamente o conceito de algarismos significativos. A corda e a roldana são considerados ideais.

Dados:

m 1 = 1,00   k g   ; m 2 = 1,60   k g   ;   θ = 53 °  

Determine:

a) O menor valor para o coeficiente de atrito estático na rampa inclinada que mantém o sistema em repouso.

b) O módulo da aceleração do sistema para μ c i n é t i c o = 1,327 e o valor da tensão na corda, se o sistema sofre um pequeno impulso que o põe em movimento.

Passo 1

Parte I

a) Calculando o coeficiente de atrito pedido:

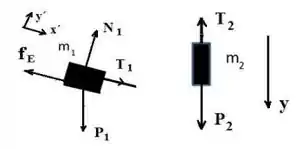
Analisando o bloco 1:

Eixo y’:

N 1 = P 1 c o s θ  

Eixo x’:

P 1 s e n θ + T 1 - f E = 0   → m 1 .   g . s e n θ + T 1 - μ E . m 1 . g . c o s θ = 0   ( 1 )

Analisando o bloco 2:

Eixo y:

P 2 = T 2

Como T 1 e T 2 pertencem à mesma corda sem roldanas intermediárias:

T 1 = T 2 = P 2   ( 2 )

Substituindo (2) em (1), temos:

m 1 .   g . s e n θ + m 2 . g - μ E . m 1 . g . c o s θ = 0

μ E = m 1 .   g . s e n θ + m 2 . g m 1 . g . c o s θ = 1   .   s e n 53 ° + 1,6 1   .   c o s 53 ° = 4  

Passo 2

a) Calculando a aceleração e a força pedidas:

Do bloco (1):

m 1 .   g . s e n θ + T - μ C . m 1 . g . c o s θ = m 1 .   a   ( 1 )

Do bloco (2):

m 2 . g - T = m 2 .   a   → T = m 2 .   g - m 2 .   a   ( 2 )

Substituindo (2) em (1):

m 1 .   g . s e n θ + m 2 .   g - m 2 .   a   - μ C . m 1 . g . c o s θ = m 1 .   a

a = s e n θ -   μ C . . c o s θ . m 1 + m 2 m 1 + m 2 . g = 1 . s e n 53 ° - 1,327 . c o s 53 ° + 1,6 1 + 1,6 . 9,8

a = 6,03   m / s 2

T = 1,6   .   9,8 - 1,6   .   6,03 = 6,03   N

Resposta

Parte I

  1. μ E = 4
  2. a = 6,03   m / s 2   ;   T   = 6,03   N  

Exercícios de Livros Relacionados

Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de
Um operário aplica uma força constante de módulo 85N a uma caixa de 40k g que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de 1,4m , sua vel
Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e