Dois blocos de massas e estão em contato entre si, com o bloco sobre o bloco . Um fio ideal ligado ao bloco tem sua outra extremidade presa em um suporte vertical fixo. O bloco encontra-se inicialmente em repouso sobre uma superfície horizontal sem atrito, e num dado instante é puxado por uma forca horizontal constante, como mostra a figura. A força tem módulo suficiente para deslocar o bloco . Sabe-se que existe atrito entre as superfícies de contato entre os blocos, cujo coeficiente de atrito cinético é .
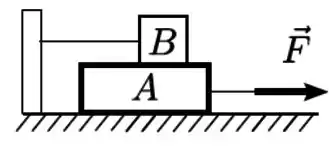
Considere que: o fio permanece esticado durante todo o tempo; a resistência do ar é desprezível; a gravidade tem módulo conhecido.
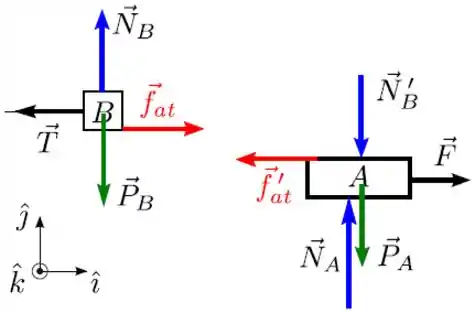
a) Faça o diagrama das forças que atuam sobre os blocos e separadamente;
b) Determine a aceleração com que o bloco se move e o módulo da tração que age no fio preso ao bloco ;
c) Determine o módulo da força resultante que o bloco exerce sobre o bloco .
Passo 1
a)
Sempre que tivermos blocos encostando um no outro, além do mais com atrito, temos que ter a 3ª lei de Newton em mente: toda força tem sua reação. Mas é claro que só vamos considerar as forças de reação que atuarem nos blocos.
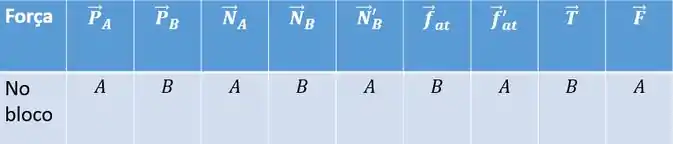
Assim, as forças atuando nos blocos são:
- as forças peso e
- as forças normais: pro bloco A, realizada pela superfície e pro bloco B, realizada pelo próprio bloco A.
- a força no bloco A, de reação a
- a força de atrito no bloco B, realizada pelo bloco A
- a força no bloco A, de reação a
- a força de tração do fio, no bloco B
- e claro, a força , no bloco A
São tantas forças que pra gente não se perder eu montei uma tabelinha:
Passo 2
Então os diagramas das forças são:
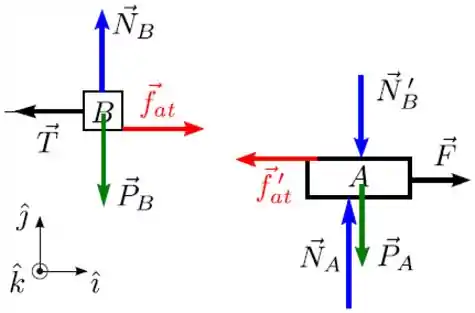
Passo 3
b)
Falou em aceleração meu amigo, não tem erro, vamos usar a 2ª lei de Newton!
O bloco A se mexe somente no sentido do eixo , então a 2ª lei de Newton pra ele fica:
Passo 4
E como adotamos o sentido positivo sendo pra direita, no eixo , e pra cima, no eixo , em módulo isso dá:
E pela 3ª lei de Newton, , e , então:
Passo 5
O bloco B fica parado, então a resultante de forças atuando nele dá zero, tanto no eixo quanto no eixo :
Em módulo, obtemos:
Passo 6
Queremos o módulo da tração e achamos .
A força de atrito é dada pelo produto do coeficiente de atrito cinético com a normal, então como ela atua no bloco B, temos:
Passo 7
Ainda falta achar a aceleração do bloco A! Agora ficou fácil, porque achamos
Ou seja,
Passo 8
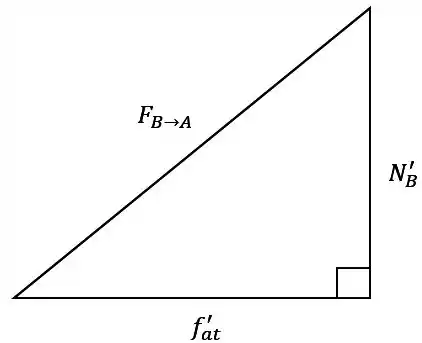
c)
As forças que o bloco B faz no A são e . Então a força total do bloco B sobre o bloco A é:
Passo 9
Essas 2 forças são perpendiculares, então pra achar o módulo da força resultante, basta aplicar Pitágoras, saca:
Resposta
a)
b)
c)