Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
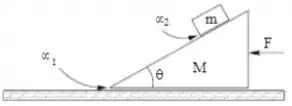
- Faça o diagrama de forças nos dois blocos, enquanto há movimento, mas o de cima não se move sobre o de baixo. Marque quais dessas forças são pares de ação e reação. Faça outro desenho e separe os blocos para maior clareza.
Passo 1
Oi, tudo bem?

Nesse primeiro item o problema pede pada separar os dois corpos e indicar todas as forças que agem sobre eles. E identificar os pares ação e reação das forças entre os blocos. Então é isso que vamos fazer aqui!
Conhecemos algumas forças: força peso, normal, de atrito, força externa, elástica, centrípeta... e a ideia é identificar nessa situação quais delas estão presentes

Vamos começar?
Obs: quando o par ação-reação estiver entre os blocos, essas forças vão estar desenhadas bem bonitinhas, mas quando o par for em outro corpo, relaxa que vou indicar onde vai estar para você entender ok?
Passo 2
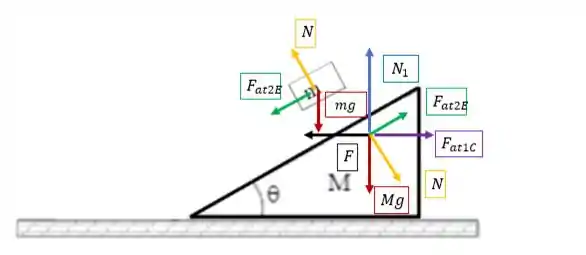
Vou começar por duas forças bem conhecidas: força peso e força normal! Em ambos os blocos temos a força peso, cada um com valor diferentes, pois os blocos têm massas diferentes e apontam verticalmente para baixo na direção da Terra.
Esses vetores estão representados em vermelho. Seus pares reação estão no centro da Terra e apontam verticalmente para cima, na direção de cada caixa:
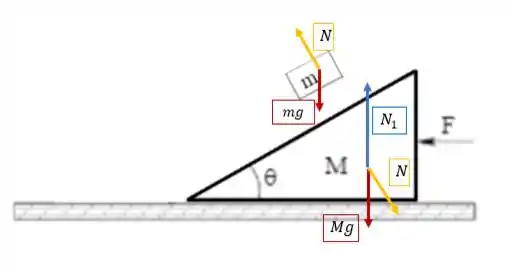
E aqueles outros vetores (azuis e amarelo)? Eles representam as normais! Isso mesmo! Como temos sustentação em ambos os blocos, há dois tipos de força normal: entre a mesa e o bloco e entre os dois blocos!
A força representada pelo vetor azul : é a força que a mesa faz para sustentar o bloco de massa (que tem nele também o bloco ) e seu par reação está sobre a mesa, verticalmente para baixo.
Os outros dois vetores em amarelo representam a força de sustentação que os blocos fazem entre si, pois o bloco está apoiado no bloco , e vice-versa. Eles formam um par ação-reação: são forças de mesma natureza, agem em corpos distintos, têm mesmo módulo e direção, e sentido oposto.
Beleza até aqui?

Passo 3
Agora vamos para as forças de atrito e a força externa? Como comentei lá no passo 1, temos dois tipos de atrito: o atrito da mesa com o bloco e o atrito entre os blocos e .
O atrito entre os blocos é o que impede que o bloco deslize. No bloco ele aponta contra o movimento que ele teria se subisse, ou seja, para baixo. Já sua reação está no bloco , e tem mesmos módulo e direção, mas sentido oposto. Essas forças estão representadas pelos vetores em verde:
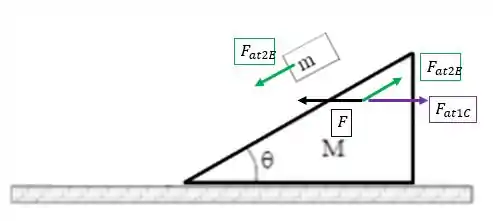
E aquele outro vetor em roxo? É o atrito que a mesa faz no bloco , tentando resistir ao movimento. Como a força aponta para a esquerda, a força de atrito vai apontar para a direita. Seu par reação está na mesa e aponta para a esquerda.
Tranquilo?

Por fim a força externa é a força que é aplicada paralela ao solo, para a esquerda. Essa força está representada em preto.
Agora vamos juntar todas essas forças em um único diagrama!
Passo 4
Agora vamos juntar todos esses vetores em um único desenho:
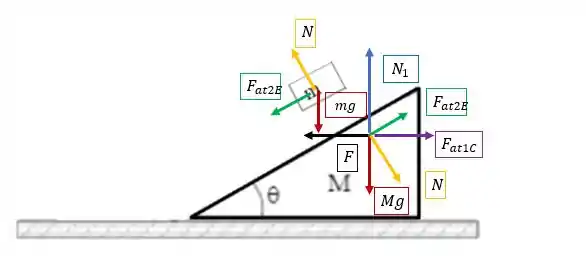
aí estão representadas as forças:
- Em vermelho: força peso dos blocos (reação está na Terra)
- Em amarelo: força normal de apoio entre os blocos (ação e reação em cada bloco)
- Em azul: força normal que a mesa faz no bloco (sua reação está na mesa)
- Em verde: força de atrito entre os blocos (reação também em cada bloco)
- Em roxo: força de atrito que a mesa faz em cima do bloco (a reação está na mesa)
- Em preto: força externa (sua reação está no agente externo dessa força)
Apenas as forças e tem seus pares ação-reação entre os dois blocos, os pares das outras forças são em corpos em torno da dinâmica.
Fazer um diagrama de forças é o primeiro passo para determinar o valor das forças que estão envolvidas em um problema. Nos próximos itens vamos, a partir desse diagrama, determinar os valores das forças, da aceleração e caracterizar por completo essa dinâmica. Mas isso é cena dos próximos capítulos, por enquanto é só!
E é isso!
Espero ter ajudado!
Resposta