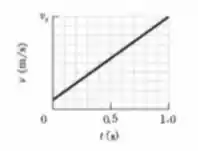
Um bloco de é empurrado sobre um piso por uma força horizontal constante de módulo . A figura abaixo mostra a velocidade do bloco em função do tempo quando o bloco se desloca sobre o piso ao longo de um eixo . A escala vertical do gráfico é definida por . Qual é o coeficiente de atrito cinético entre o bloco e o piso?
Passo 1
Oi galera, tudo bem? Esta é uma questão que envolve a aplicação da segunda lei de Newton e também do conhecimento de cinemática. Mas relaxa, vou ajudar você aqui!

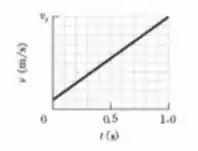 Vamos iniciar este problema analisando o gráfico e extraindo a partir das informações dele a aceleração do corpo
Vamos iniciar este problema analisando o gráfico e extraindo a partir das informações dele a aceleração do corpo
Como o corpo está se deslocando com a aceleração constante, então podemos determinar a aceleração usando a seguinte relação:
Pelo gráfico temos os pontos e , assim:
Aqui foi a parte da cinemática que falei! Daqui rpa frente é Newton na veia!

Então temos a aceleração, a massa dele e a força com que esse bloco é puxado. E o problema pede o coeficiente de atrito entre a mesa e o bloco.
A ideia aqui é aplicar a segunda lei de Newton para determinar as equações de força e delas calcular o coeficiente de atrito.
Vamos lá?
Passo 2
Com a aceleração em mãos, vamos fazer o diagrama de corpo livre:
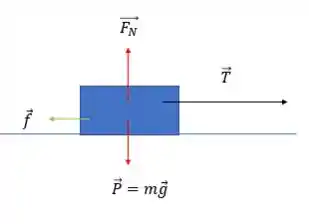
E agora podemos aplicar a segunda lei de Newton na direção do movimento:
Isolando :
Vamos guardar essa equação!!
O problema nos fornece o módulo da força e a massa do bloco, a aceleração foi calculada anteriormente e o que queremos é o coeficiente de atrito cinético. Para conectar todas essas variáveis, devemos lembrar da definição de força de atrito
Passo 3
Para determinar a normal, devemos aplicar a segunda lei de Newton para o eixo perpendicular ao movimento:
Como este eixo é perpendicular ao movimento , assim:
Isolando :
Então a força de atrito é:

Passo 4
Por fim, vamos substituir então a força de atrito na equação que guardamos no passo 2 () e igualar:
Isolando e substituindo os valores conhecidos:
E é isso! Espero ter ajudado!