Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
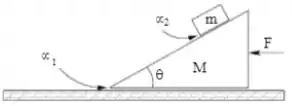
2) calcule o valor da normal entre os blocos nessa situação
Passo 1
Oi, tudo bem?

No primeiro item dessa questão foi pedido o diagrama de forças dos dois blocos.
Nesse segundo item o problema pede para encontrarmos o valor da normal entre os blocos
Para isso acontecer, a componente vertical da força resultante sobre os blocos deve ser nula, bem como diz no enunciado. Dessa condição irá sair uma equação. E a única aceleração será na horizontal, então vamos aplicar a segunda lei de Newton para achar qual será a aceleração mínima.

Certo? Mas calma, vou fazer junto com você! Vou resgatar do item 1 dessa prova o diagrama de forças, assim fica mais fácil você se localizar nas forças:
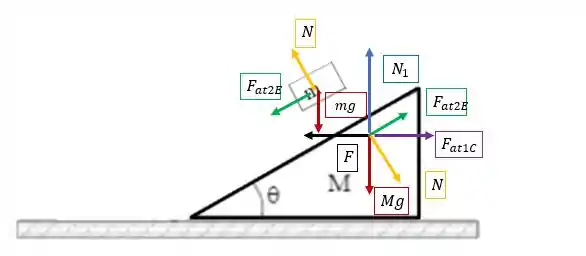
A ideia aqui é, a partir desse diagrama de forças, verificar para qual bloco encontramos a força com maior facilidade, usando a segunda lei de Newton e as condições que o problema pede!
Passo 2
Como o bloco menor tem menos forca agindo sobre ele, ele é quem vou escolher para encontrar a normal . Lembrando que esse bloco está na eminência de se movimentar verticalmente, mas por enquanto, ele só descreve um movimento horizontal junto com o bloco maior.

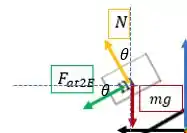 Sendo assim, temos um equilíbrio de forças atuando na vertical. Vou utilizar a força peso como referência para o eixo vertical, assim o sistema de coordenadas está representado pelas linhas pontilhadas no desenho aqui:
Sendo assim, temos um equilíbrio de forças atuando na vertical. Vou utilizar a força peso como referência para o eixo vertical, assim o sistema de coordenadas está representado pelas linhas pontilhadas no desenho aqui:
Para cima temos a componente vertical da força e para baixo temos a força peso e a componente vertical da força de atrito entre os blocos .
Temos o equilíbrio na vertical, então:
A força de atrito tem a ver com a normal e o coeficiente de atrito estático :
Pronto! Agora temos uma equação que envolve as constantes e e a única variável é a força !
#partiuisolarN

Passo 3
Do passo anterior encontramos a seguinte equação de equilíbrio:
Agora é só colocar em evidência:
Prontinho! Encontramos a normal que atua entre os blocos!
E é isso!
Espero ter ajudado!