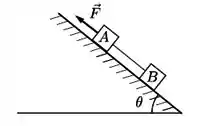
Dois blocos A e B de massas iguais a , são ligados entre si por um fio ideal e colocados, em repouso, sobre uma rampa inclinada de um ângulo em relação à horizontal. Os coeficientes de atrito cinético entre a superfície do plano inclinado e as superfícies do bloco A e do bloco B são, respectivamente, iguais a e . Num dado instante o bloco A é puxado por uma força de módulo constante, e paralela à superfície, de forma que ele passa a se deslocar superfície acima, como mostra a figura. A força tem módulo suficiente para manter os blocos em movimento e o fio esticado
- Isole os blocos e represente todas as forças que agem em cada bloco, separadamente, identificado-as;
- Determine o módulo da aceleração com que os blocos se movem;
- Determine o módulo da tração que age no fio que liga os blocos;
- Se trocarmos os blocos de posição, mantendo a mesma força aplicada sobre o bloco de cima, qual a diferença entre os novos valores de aceleração e tração em relação aos encontrados nos itens (b) e (c)? Justifique sua resposta.
Passo 1
Letra a)
A primeira parte da questão é fazer o diagrama de forças. As forças que estão presentes nos dois blocos são:
Tração: ação da força dos cabos
Peso: ação gerada pela gravidade
Atrito: contato entre as superfícies
Normal: reação do plano inclinado perpendicular a superfície.
Além dessas forças, temos também a força , mas ela só está presente no bloco A.
Desenhando fica assim:
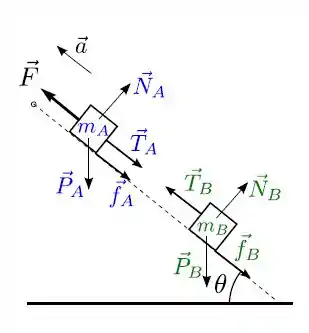
Não é nenhuma obra de Picasso, mas até que ficou bonito, né? hahahahha
Passo 2
Letra b)
Agora que ele quer saber a aceleração vamos escrever a segunda lei do nenê pra cada bloco. Lembrando que como os blocos estão ligados por uma mesma corda vamos ter que.
Por uma questão de sentido, vamos supor que o bloco está subindo. Caso essa suposição seja errada, a única diferença que vamos encontrar é o valor negativo no final da questão. Só estamos adotando um referencial
Assim a equação pro bloco fica, já decompondo todas as forças no eixo da superfice do plano inclinado:
Bloco :
Usando aquelas relações que falamos lá em cima, as duas equações ficam assim
Olha que legal agora ! Nós estamos interessados na aceleração e aquela força de tração ali não foi dada pra gente. A idéia é sumir com ela pra ficar mais fácil chegar na resposta. Uma solução pra isso é somar as duas equações !!!
Isolando o que a gente quer ficamos com a resposta !!
Passo 3
Letra c)
Para descobrirmos o valor de tração podemos usar o resultado que descobrimos na alternativa anterior!!! É só pegar uma das equações e substituir o valor da aceleração que nós achamos.
Vamos usar a segunda equação só porque tem menos termos, hehehehe
Isolando o e substituindo o valor da aceleração temos
Agora vamos dar uma organizada nisso ai porque tem muita coisa repetida que dá pra gente cortar
Até que ficou bonitinho
Passo 4
Letra d)
Bom, primeiro vamos pensar um pouco sobre a aceleração. Se lembra quando nós achamos a aceleração na alternativa la de cima?
Se você perceber essa equação não depende da força de tração entre os blocos, ou seja, mesmo que a força de tração entre os blocos mude, a aceleração deles vai ser a mesma
Passo 5
Já que ele quer saber a diferença entre as forças, vamos calcular a nova tração que eu vou chamar de
Já sabemos que a aceleração dos blocos continua igual, que as forças de trações entre eles são iguais e que a aceleração também é igual, então vamos quase usar aquela equação que usamos lá em cima.
A diferença é que agora em vez de somarmos ela, vamos diminuir uma da outra, já que não estamos interessados na aceleração do sistema.
Agora que já descobrimos o podemos fazer a diferença entre as forças