Força e Leis de Newton
Um bloco de peso está deslizando para baixo em um plano inclinado de com a horizontal. Existe atrito entre o bloco e o plano. A aceleração do bloco é de dirigida para cima ao longo do plano.
a) Desenhe o diagrama de corpo livre para o bloco durante a descida.
b) Calcule o valor do coeficiente de atrito cinético entre o bloco e o plano.
Passo 1
a)
O bloco não possui nenhuma força agindo sobre ele além da força peso e das duas forças de contato (normal e atrito).
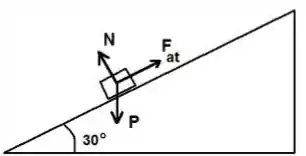
Para facilitar, escolhemos o eixo paralelo ao plano inclinado e o sentido positivo no sentido do movimento, e o eixo paralelo ao vetor da força Normal e sentido positivo no mesmo sentido da normal.
Passo 2
b)
A segunda lei de Newton neste caso fica:
Por componentes:
Eixo :
Porém . Logo:
Eixo :
Então, decompondo o peso:
Resposta
a)
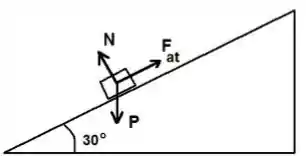
b)