Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo. O coeficiente de atrito entre os blocos e o solo é 0,2.

Desenhe um diagrama das forças que atuam em cada um dos blocos e as escreva em um referencial determinado por você.
Determine a aceleração do conjunto e as forças que atuam em cada bloco.
Se a posição dos blocos fosse trocada o que mudaria nas forças e na aceleração?
Passo 1
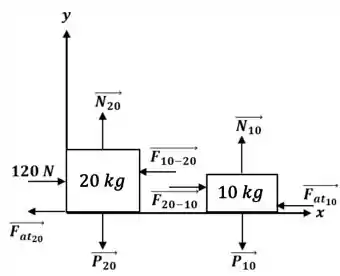
Passo 2
Vamos usar a segunda lei de Newton () para o sistema. Lembrando que o sistema não possui movimento no eixo , o peso e a normal dos blocos se anulam.
Pela terceira lei de Newton sabemos que os pares ação e reação tem o mesmo valor mas com sentidos diferentes. Portanto, , logo, elas se cancelarão no sistema, sobrando apenas.
Agora basta calcular e , vamos usar a fórmula da força de atrito ()
Como vimos no início deste item, e , portanto:
Agora podemos calcular a e a utilizando a segunda lei de Newton () para o bloco de massa igual a :
Novamente, usando para o bloco de massa igual a :
Passo 3
Mudar a posição dos blocos apenas afetará o valor das forças de ação e reação entre os blocos, mas como essas forças se cancelam no cálculo da aceleração, a aceleração será a mesma, independentemente da posição dos blocos.
Resposta
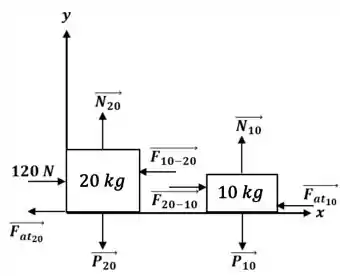
Mudar a posição dos blocos apenas afetará o valor das forças de ação e reação entre os blocos, mas como essas forças se cancelam no cálculo da aceleração, a aceleração será a mesma, independentemente da posição dos blocos.