UFRJ – Física 1 – P1 – 2019.2 – Questão 1
Uma placa é pressionada contra uma parede e sobe empurrada para cima por uma força de módulo igual ao módulo do peso da placa, mas fazendo um ângulo com o eixo OU vertical para cima, como mostra a figura.
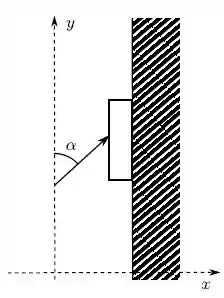
Qual a aceleração adquirida pela placa?
Passo 1
Vamos lá! Primeiramente precisamos verificar as forças que estão atuando sobre a placa.
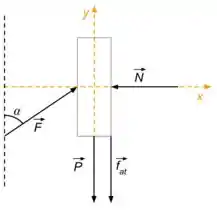
Onde é o peso da placa, é a força da parede sobre a placa, é a força que pressiona a placa contra a parede e é a força de atrito.
A força de atrito está orientada para baixo, pois o enunciado disse que a placa está subindo e, por conta disso também, é a uma força de atrito cinético.
Passo 2
Agora podemos decompor as forças nas coordenadas dadas.
Cabe ressaltar que como o movimento é apenas vertical
Portanto, sendo a componente da força no eixo , temos
Para as forças em , temos
Sendo assim
Onde
Passo 3
A força de atrito cinético é dada por
Lembrando que o enunciado disse que
E sabendo que
Podemos escrever que
Reorganizando temos