Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito Cinético

Ver Teoria
Exercício 23123456789101112131415161718192021222425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576

Enunciado

Dois corpos estão ligados por um fio que passa por uma polia conforme mostrado na figura. O suporte tem uma face inclinada ( θ = 30 ° ) e outra horizontal. O corpo A desce sobre a face inclinada enquanto o corpo B se move sobre a face horizontal (sem chegar até a polia). A superfície sobre a qual estão os corpos se caracteriza por um coeficiente de atrito estático μ s = 0,40 e um coeficiente de atrito cinético μ c = 0,25 . Considere fio e polia ideais. Assuma g = 10   m / s 2 . Aproxime 3 ≅ 1,7 . Você pode dar o resultado aproximado com uma casa decimal.

LEMBRETE: Todos os seus passos devem ser explicitados de forma clara.

(a) Faça um diagrama das forças do sistema.

(b) Sendo as massas dos corpos A e B , respectivamente, m A = 4 k g e m B = 1 k g , calcule a tração no fio.

(c) Para a mesma situação do item anterior, calcule a aceleração dos dois corpos.

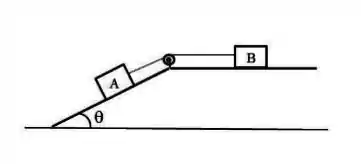
Passo 1

(a)

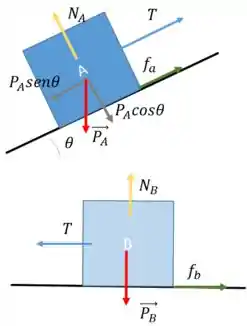
Passo 2

Para o bloco A:

I   P A c o s θ = N A

I I   F A = m A . a A = P A s e n θ - T - f A

Para o bloco B:

I I I   P B = N B

I V   F B = m B . a B = T - f B

Passo 3

Como o cabo tem comprimento fixo, as acelerações dos corpos são iguais, das equações I I e ( I V ) , temos:

P A s e n θ - T - f A m A = T - f B m B

Sabendo que f A = μ C . N A = μ C . P A c o s θ e f B = μ C . N B = μ C . P B , temos:

m A . g . s e n 30 o - T - μ C . m A . g . c o s 30 o m A = T - μ C . m B . g m B

Substituindo os dados do enunciado:

4.10.0,5 - T - 0,25.4 . 10 . 1,7 2 4 = T - 0,25.1 . 10 1

T = 4,3 N

Passo 4

Para as acelerações dos corpos, basta que substituamos o resultado obtido para T na equação ( I I ) ou ( I V ) :

m B . a B = T - μ C . P B

a B = 4,3 - 0,25.10 = 1,8 m / s 2

Resposta

T = 4,3 N

a A = a B = 1,8 m / s 2

Exercícios de Livros Relacionados

Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de
Um operário aplica uma força constante de módulo 85N a uma caixa de 40k g que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de 1,4m , sua vel
Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e