[Enunciado comum às Questões 3 e 4]
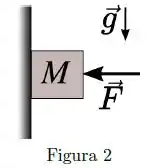
Uma força atua horizontalmente sobre um bloco de massa e que se encontra apoiado em uma parede vertical, como mostrado na figura. O coeficiente de atrito estático entre o bloco e a parede é . Considere o módulo da aceleração gravitacional no local .
[Questão 4]
Para uma força aplicada de módulo , o bloco desce com aceleração de módulo . O coeficiente de atrito cinético entre o bloco e a parede é igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Vamos começar com o Diagrama do Corpo Livre:
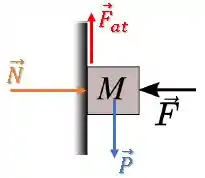
Lembrando que como o bloco está deslizando, a força de atrito atuando sobre ele é cinética.
Na horizontal, temos um equilíbrio de forças, já que não há nenhuma aceleração nessa direção:
Mas o enunciado nos deu que o módulo de é , então:
Na vertical, o bloco está descendo com uma aceleração de , então vamos considerar um referencial positivo para baixo:
Passo 2
Nosso objetivo é achar o coeficiente de atrito cinético .
A força de atrito cinética que atua sobre o bloco pode ser calculada com:
Então, igualando as duas expressões para a :
Achamos que :
Substituindo os valores, temos:
Ficamos com a letra (f).
Resposta
Letra (f)