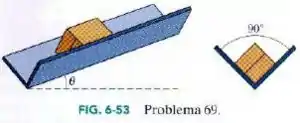
Na Fig. 6-53, um caixote escorrega para baixo em uma vala cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é . Qual é a aceleração do caixote em termos de , e ?
Passo 1
Temos aqui uma situação especial, onde existem duas superfícies que oferecem atrito ao movimento do corpo. Mas não fique bolado, nada mudou. Vamos fazer o diagrama de corpo livre baseado na segunda imagem apresentada no enunciado.
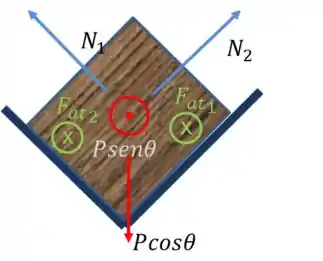
Beleza, temos todas as forças expressas no diagrama acima, mas temos agora, diferente das outras vezes, 3 eixos pra analizar. Vamos usar os seguintes eixos como referência:
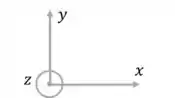
Passo 2
Temos movimento, ou seja, temos aceleração somente no eixo , portanto, podemos aplicar a primeira lei de Newton nos eixos e . Decompondo as forças e no eixo , temos:
Para facilitar, vamos chamar o valor das normais de , portanto:
Passo 3
Já no eixo , temos:
Usando o resultando obtido anteriormente:
Passo 4
Habemus movimento no eixo ! Nos foi dito que o caixote está descendo, portanto, usaremos a segunda lei de Newton:
Substituindo as expressões para o peso e para a força de atrito cinético, temos:
Resultados anteriores dizem que:
Substituindo o valor de e , portanto:
Chegamos finalmente ao valor de :