[ENUNCIADO COMUM ÀS QUESTÕES 5 e 6]
Um bloco de massa está em movimento ao longo da superfície de um plano inclinado que faz um ângulo com a horizontal e está submetido a uma força .
[QUESTÃO 6]
A massa do bloco é , a força aplicada tem módulo e o coeficiente de atrito cinético é . Considere , e . O módulo da força de atrito atuando sobre o bloco é
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Nosso objetivo é descobrir o módulo da força de atrito .
Nós sabemos pelo enunciado que o bloco está em movimento, isso significa que a a força de atrito que atua sobre ele é uma força de atrito cinético.
A força de atrito cinético é dada por:
Então, no fundo só precisamos descobrir a força normal que conseguimos calcular a .
Passo 2
Fazendo o diagrama de forças, assumindo que o bloco desliza para baixo ( para cima):
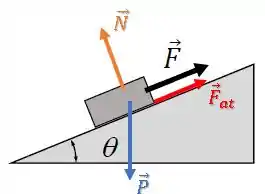
Podemos decompor a força peso na direção paralela e perpendicular à superfície da rampa.
Para isso, vamos usar o ângulo :
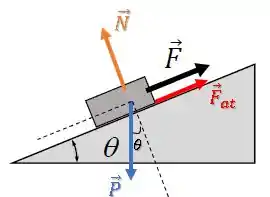
Ficamos com as componentes:
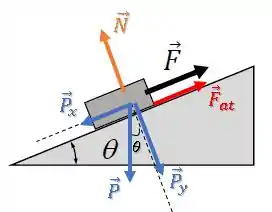
Passo 3
Para achar o módulo de da força normal , vamos aplicar a segunda lei de newton na direção perpendicular à rampa:
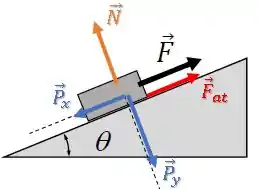
Nessa direção, o bloco está em equilíbrio, pois a aceleração é unicamente na direção paralela à rampa:
A componente é dada por:
Passo 4
Voltando à expressão da força de atrito, temos:
Ficamos com a alternativa (h).
Resposta
Letra (h)