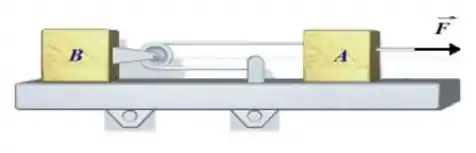
Parte I - Considere o sistema físico na figura abaixo.
Os blocos possuem massas e . A roldana e os fios são ideais. Existe atrito entre o piso e os blocos A e B com coeficiente de atrito cinético . A força que puxa o bloco A tem valor . Devido à ligação entre os fios e a roldana, a aceleração do bloco B é duas vezes menor que a do bloco A.
- Faça os diagramas de forças dos blocos A, B e da roldana.
- Encontre o valor da aceleração do bloco A () e do bloco B ().
- Encontre o módulo da tensão e da força que a roldana faz sobre o bloco B
Passo 1
Parte I
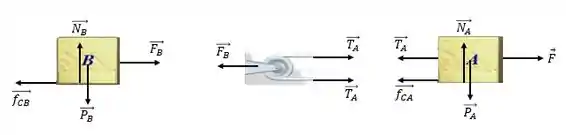
a) Traçando o diagrama de corpo livre:
Passo 2
b) Calcularemos as acelerações dos blocos A e B.
Analisando o bloco A:
Eixo Y:
Eixo X:
Analisando a roldana:
Eixo X:
Analisando o bloco B:
Eixo Y:
Eixo X:
Do enunciado, temos que:
Somando (1) e (3), temos:
Substituindo (4) em (5), vem:
Passo 3
c) Calcularemos os valores de e .
Da equação (3), temos:
Da equação (2), temos:
Resposta
Parte I
Exercícios de Livros Relacionados
Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de
Um operário aplica uma força constante de módulo 85N a uma caixa de 40k g que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de 1,4m , sua vel
Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e