Considere duas rampas inclinadas, perpendiculares entre si, e que formam com o solo um triângulo retângulo, como ilustra a figura. Dois blocos e de mesma massa m estão, inicialmente, em repouso nos pontos mais altos de cada rampa. O bloco encontra-se sobre a rampa menos inclinada, a da direita na figura, que forma um ângulo com a horizontal e, nela, o atrito é desprezível. Em contrapartida, o coeficiente de atrito cinético entre a rampa da esquerda e o bloco , que desliza sobre ela é . Verifica-se, então, que os blocos deslizam sobre as rampas.
a) Supondo que ambos os blocos iniciem seus movimentos de descida no mesmo instante e que atinjam o solo simultaneamente, determine o coeficiente de atrito . Sua resposta deve ser dada em termos das grandezas: , e .
b) Discuta o resultado do item anterior para .
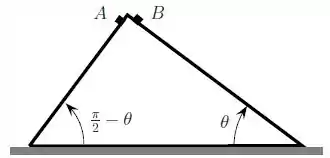
Passo 1
Vamos primeiro fazer o diagrama de corpo livre e aplicar a segunda lei de Newton para os dois blocos.
Na rampa da direita, temos as seguintes forças sobre o bloco :
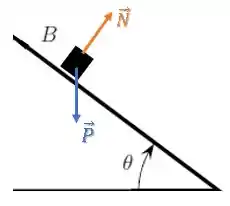
Podemos decompor a força peso em suas componentes paralela e perpendicular à rampa:
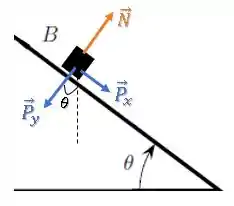
Na direção paralela à rampa, temos:
Cortando as massas:
Passo 2
Já na rampa da esquerda, vamos fazer o mesmo procedimento com o bloco , porém agora temos uma força de atrito contrária ao movimento:
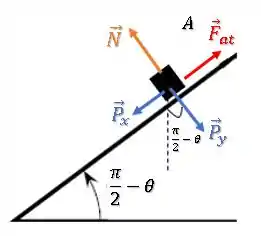
Na direção paralela à rampa, temos:
A componente é:
A força de atrito cinética é dada pelo coeficiente de atrito cinético vezes a força normal :
Podemos ainda olhar para a direção perpendicular à rampa para obter outra relação com a força normal (desconhecida).
Na direção perpendicular, temos um equilíbrio de forças pois não há aceleração nessa direção:
Substituindo a força normal na primeira equação, temos:
Cortando as massas, temos:
Passo 3
Até aqui, fizemos o passo a passo de sempre para uma questão de plano inclinado.
Queremos saber na letra (a), qual o coeficiente de atrito que faz os blocos chegarem ao chão ao mesmo tempo.
Sabemos que os dois blocos descem com acelerações e , logo eles realizam um movimento retilíneo uniformemente variado (MUV).
Podemos usar a equação de movimento do MUV:
Já temos uma expressão para a aceleração de cada um deles, porém temos que achar a distância percorrida por cada um deles.
A distância será diferente simplesmente porque a inclinação da pista é diferente.
Passo 4
Olhando para o triângulo retângulo, queremos obter uma expressão para a distância percorrida por e por :
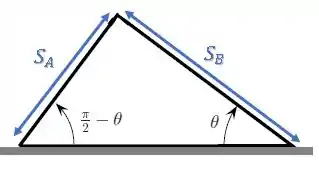
Vamos relacionar as duas com a altura da rampa e os ângulos respectivos:
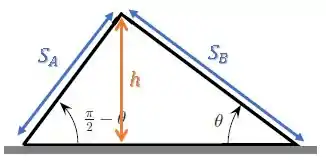
Para a distância percorrida por , temos:
Enquanto para a distância percorrida por , temos:
Passo 5
Agora, vamos voltar à equação de movimento:
Vamos considerar a origem no ponto de partida de ambos os blocos:
Sabemos também que ambos parte do repouso , ficamos com:
Para o bloco , temos:
Para o bloco , temos:
Passo 6
Queremos a situação onde os blocos atinjam o chão ao mesmo tempo, logo, vamos igualar as expressões pelo tempo :
Passo 7
Agora vamos substituir as expressões que temos e isolar o .
Para facilitar a visualização, vamos chamar de :
Cortando e , temos:
Isolando , temos:
Reescrevendo como :
Pronto! Está com a cara feia mas achamos a resposta.
Caso a gente queira uma resposta mais bonitinha, podemos utilizar algumas relações trigonométricas para ajeitar nossa resposta...
Passo 8
A primeira relação é que e são ângulos complementares, ou seja, somam :
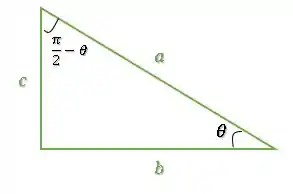
Assim, temos que:
Colocando todos os “senos” e “cossenos” em função apenas de , ficamos com:
Por últimos, podemos usar que:
Assim, nossa expressão fica:
Ou seja, chegamos no mesmo resultado, porém com outra identidade trigonométrica.
Passo 9
Já na letra (b), queremos analisar para o caso do ângulo ser .
Cara, pensa comigo...
O ângulo é o mesmo que . Ou seja nesse caso os dois lados da rampa teriam a mesma inclinação:
Como ambos têm a mesma inclinação, porém apenas um deles tem atrito, parece difícil que eles consigam chegar juntos na base da rampa, não é mesmo?
Vamos substituir o valor de na expressão de e ver o que achamos:
Ou seja, achamos que para que os dois blocos cheguem na base da rampa com o mesmo tempo, o coeficiente de atrito deve ser nulo (não pode ter atrito).
Resposta
(a)
Ou
Ou
(b) Para que os dois blocos cheguem na base da rampa com o mesmo tempo, o coeficiente de atrito deve ser nulo (não pode ter atrito).