Um cachorro de massa caminha preso a uma coleira inextensível e de massa desprezível. A outra extremidade da coleira está amarrada a uma mola de constante elástica , que pode distender-se sem atrito ao longo de um tubo horizontal. A outra extremidade da mola está fixa numa parede. O coeficiente de atrito entre o cachorro e o chão é e na situação mostrada na figura a mola está com a máxima distensão e o cachorro está na iminência de escorregar. Nesta situação:
a) Monte o diagrama de forças agindo sobre o cachorro;
b) Qual é a máxima distensão da mola?
c) Qual a tração na corda?
NOTA: Nos itens (b) e (c), dê sua resposta em função das variáveis descritas no problema e de constantes, somente.
Passo 1
a)
O que faz com que a corda não joga o cachorro para trás é a força de atrito estática. Como diz o enunciado, ele está na iminência de escorregar, ou seja, está na força de atrito estática máxima.
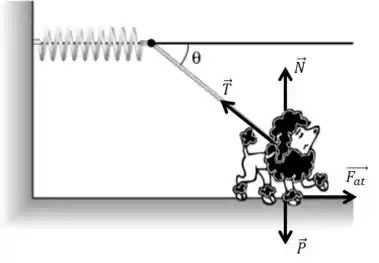
Passo 2
b)
Primeiramente temos que decompor a tração em e .
Entretanto, a magnitude da tração da corda na horizontal está ligada a força elástica da mola, já que eles estão conectados. Então podemos dizer que:
Agora falta nós acharmos a tração. Fazendo o equilíbrio de forças no cachorro na horizontal:
Substituindo na equação anterior:
Mas não podemos dar essa resposta, pois a força normal não foi dada no enunciado. Precisamos colocar ela em função de coisas que foram dadas no enunciado. Para isso, vamos usar nosso último recurso, fazer o equilíbrio das forças no cachorro na vertical.
Agora voltando lá no equilíbrio que fizemos na horizontal, nós tínhamos encontrado:
Substituindo:
Agora sim! Só substituir na nossa equação de distensão da mola.
Passo 3
c)
Basta utilizar a equação que encontramos no item anterior ao relacionar com :
Agora é só substituir o valor de que encontramos no item anterior:
Resposta
a)
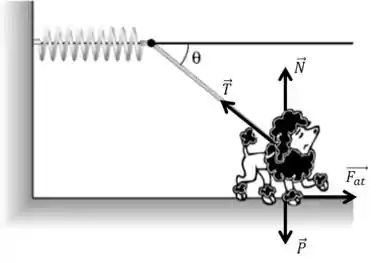
b)
c)