UFMG – Fundamentos de Mecânica – P1 – Questão P2.1
Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
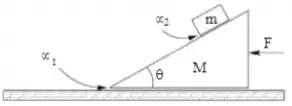
3) calcule a aceleração máxima do conjunto
Passo 1
Oi, tudo bem?
Nos itens anteriores foi pedido o diagrama de forças dos dois blocos e o valor da força normal entre os blocos. Os resultados foram esses aqui:
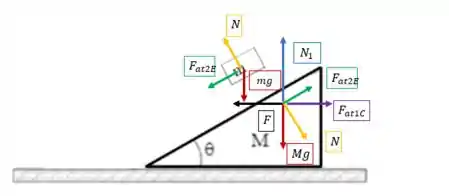
E eu trago esses resultados pois eles irão nos ajudar a resolver o problema da vez! Agora o problema pede para encontrarmos a aceleração!
O bloco menor é o que tem menos forças agindo sobre ele, então é ele que vou escolher para aplicar a segunda lei de Newton! Lembrando que como o sistema se movimenta junto, a aceleração é igual para os dois blocos, então é legal você escolher um bloco que esteja com menos força para facilitar a vida!
Beleza? Vamos começar?
Passo 2
O bloco de massa m está em equilíbrio na vertical, e foi daí que encontramos o valor da força normal . Mas na horizontal ele está sendo acelerado! Na horizontal agem duas forças: a componente horizontal da força normal (em amarelo) e a componente horizontal da força de atrito entre os blocos (em laranja) :
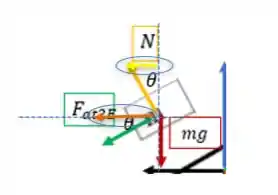e essas duas forças são responsáveis pela aceleração que esse bloco está sendo submetido! Daí da segunda lei de Newton
Tranquilo?
Passo 3
A componente da normal pode ser escrita em termos de (expressão que já conhecemos) e o ângulo . A força de atrito é o produto da normal pelo coeficiente de atrito entre os blocos e sua componente horizontal tem um multiplicado. Então agora é só substituir:
E a equação da segunda lei fica assim:
E a aceleração fica assim:
É isso? Ainda não!
Passo 4
Como calculamos a normal em termos das constantes dadas no problema () então precisamos substituir na aceleração:
Mas:
Então
Podemos ainda cortar os m’s:
Agora sim! Esse é o valor da aceleração do sistema!
E é isso!
Espero ter ajudado!