Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito Cinético

Ver Teoria
Exercício 51234678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576

Enunciado

Os blocos A , B e C são dispostos como indicado na figura abaixo e ligados por cordas de massas desprezíveis. A massa de A e de B são iguais a m . O coeficiente de atrito cinético entre cada bloco e a superfície é igual a μ . O bloco C desce com velocidade constante. a) Desenhe dois diagramas de corpo livre separados mostrando as forças que atuam sobre A e sobre B . b) Ache a tensão na corda que liga o bloco A e B . c) Qual é o peso do bloco 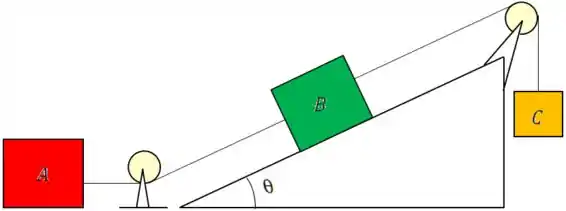C ?

Passo 1

a)

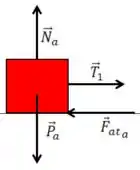
Para o bloco A

Vamos responder as perguntas do passo a passo para colocar as forças

  • A massa dele é considerada?

    • Sim, ele tem massa.

  • Ela esta encostada em alguma superfície?

    • Sim, o bloco está em contato com o chão.

  • Tem algum fio?

    • Sim, existe um fio.

  • Tem mola?

    • Não, não existe mola atuando.

  • Tem atrito?

Sim, existe atrito.

Como o bloco C está caindo isso faz com que o bloco A esteja indo para direita, ou seja, a força de atrito é contraria a isso, apontando para esqueda.

Então seu DCL fica

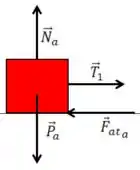
Passo 2

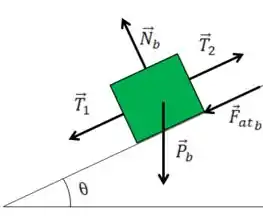
Para o bloco B

Vamos responder as perguntas do passo a passo para colocar as forças

  • A massa dele é considerada?

    • Sim, ele tem massa.

  • Ela esta encostada em alguma superfície?

    • Sim, o bloco está em contato com a superfície inclinada.

  • Tem algum fio?

    • Sim, existe um fio.

  • Tem mola?

    • Não, não existe mola atuando.

  • Tem atrito?

Sim, existe atrito.

Como o bloco C está caindo isso faz com que o bloco B esteja subindo o plano inclinado, ou seja, a força de atrito é contraria a isso, apontando para baixo.

Então seu DCL fica

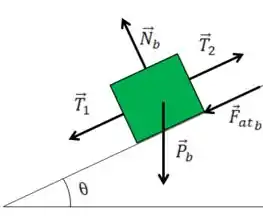
Passo 3

b)

Os dados do problema são

D a d o s m μ θ g

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

Agora devemos fazer o equilíbrio em cada bloco, começando pelo bloco A . Vamos fazer isso porque no bloco A a única força que atua no e i x o   x é T 1

Como ele está com velocidade constante, ele está em equilibrio em todos os movimentos.

No e i x o   y

N a = P a

N a = m g

Passo 4

No e i x o   x

T 1 = F a t a

T 1 = N a . μ d

T 1 = m g μ

Passo 5

c)

Para acharmos o peso do bloco C , devemos fazer o DCL dele.

Vamos responder as perguntas do passo a passo para colocar as forças

  • A massa dele é considerada?

    • Sim, ele tem massa.

  • Ela esta encostada em alguma superfície?

    • Não, o bloco não está apoiado em nenhuma superfície.

  • Tem algum fio?

    • Sim, existe um fio.

  • Tem mola?

    • Não, não existe mola atuando.

  • Tem atrito?

Não, não existe atrito.

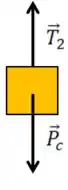
Como ele está com velocidade constante, ele está em equilíbrio em todos os movimentos.

No e i x o   y

T 2 = P c

Então para acharmos o peso de C , devemos achar T 2 . Para isso vamos fazer o equilíbrio do bloco B . Vamos primeiro fazer o DCL como normalmente escrevemos para plano inclinado.

Passo 6

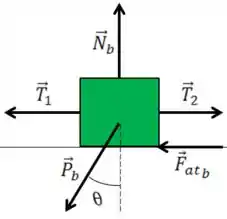
Passo 7

No e i x o   y

N b = P b y

Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.

P b y = P b . cos ⁡ θ = m g cos ⁡ θ

N b = m g cos ⁡ θ

Passo 8

No e i x o   x

T 2 = P b x + T 1 + F a t b

Devemos encontrar a sua componente horizontal usando a “regra do COlado, SEparado”.

P b x = P b . sen ⁡ θ = m g sen ⁡ θ

T 2 = m g sen ⁡ θ + T 1 + N b μ

T 2 = m g sen ⁡ θ + m g μ + m g cos ⁡ θ μ

T 2 = m g sen ⁡ θ + μ + cos ⁡ θ μ

Passo 9

Teremos então

T 2 = P c

P c = m g sen ⁡ θ + μ + cos ⁡ θ μ

Resposta

  2. T 1 = m g μ
  3. P c = m g sen ⁡ θ + μ + cos ⁡ θ μ

Exercícios de Livros Relacionados

Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de
Um operário aplica uma força constante de módulo 85N a uma caixa de 40k g que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de 1,4m , sua vel
Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e