USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 57
Um carrinho desliza, a partir do repouso, do alto de uma montanha russa de de altura, com atrito desprezível. Chegando ao sopé da montanha, ele é freado pelo terreno coberto de areia, parando em . Qual é o coeficiente de atrito cinético entre o carrinho e a areia?
Passo 1
Fala aí galera, tudo beleza?
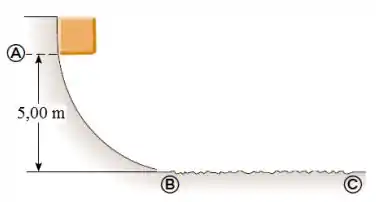
Nessa questão temos um carrinho deslizando de uma montanha do ponto ao ponto da figura, quando passa a atuar um atrito que lhe faz parar em . O enunciado quer que a gente determine o coeficiente de atrito nesse segundo trecho.
Bom, vamos pensar juntos pessoal. Qual o tipo de movimento que o bloco realiza nesse segundo trecho?
É um Movimento retilíneo uniformemente variado. No MRUV a velocidade é dada por:
Sabemos que depois de o bloco para, ou seja:
Daí, pra descobrir a aceleração precisamos apenas , que é a velocidade com que o bloco chega ao ponto .
Para fazer isso podemos usar a conservação da energia, já que no primeiro trecho não há forças dissipativas (o atrito é desprezível).
Vem com o RA que tudo vai ficar bem claro 😊
Passo 2
Bom, vamos usar a conversação da energia para calcular a velocidade com que o bloco chega ao ponto . Temos que:
Como o bloco é largado em a partir do repouso, temos:
E, considerando a referência da altura no nível do ponto , temos:
Assim:
Logo:
Massa!
Passo 3
Essa velocidade é justamente a velocidade inicial do MRUV realizado de a . Assim, podemos escrever:
Portanto:
Logo:
Massa! Encontramos a aceleração, mas como encontrar o coeficiente de atrito?
É que no movimento de até a única força horizontal que age no corpo é o atrito cinético. Assim, vale que:
Portanto:
Como o corpo está em equilíbrio na vertical:
Substituindo, vem que:
Prontinho!! Matamos a questão!
Espero que vocês tenham entendido bem direitinho 😉