Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
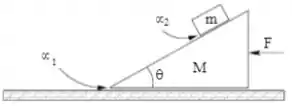
4) determine o valor máximo da força
Passo 1

E agora o problema pediu o valor máximo da força ! Nos itens anteriores foi pedido para desenhar o diagrama de forças, calcular a aceleração e a força normal entre os blocos, e eu acho que esses resultados são muito bem-vindos aqui, saca só:
O diagrama de forças vai nos ajudar a entender quais forças agem para o movimento acontecer em cada um dos blocos:
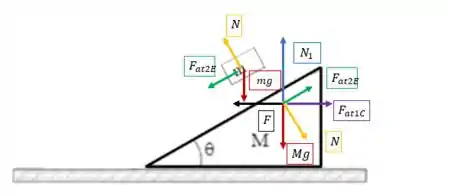
Como queremos saber o valor de , vamos olhar com carinho para o bloco maior. O vetor força é aquele em preto!
Também temos o valor da força normal que age entre os blocos (aquele vetor amarelo do diagrama), e seu valor é:
E por fim, mas não menos importante, temos o valor máximo da aceleração! (máximo porque se for maior que esse valor o bloco menor vai SUBIR sobre o plano, e não queremos que isso ocorra)
São esses os resultados dos itens anteriores! Agora o problema pede o valor de , bom a força externa está aplicada no bloco maior, então a ideia aqui é isolar ele e aplicar a segunda lei (e aqui entra os resultados anteriores, ajudando a gente!)
A força é na horizontal, assim como a aceleração. Então temos uma situação de equilíbrio na vertical (guardem isso!)

Então é isso:
- isolar o bloco no diagrama
- aplicar a segunda lei na horizontal (com a aceleração que temos)
- aplicar a primeira lei (equilíbrio) na vertical
- com essas duas equações achar a força !
Vamos começar?

Passo 2
Agora vamos isolar o bloco , traçar eixos cartesianos ao longo da força peso (que é vertical) e da força (que é horizontal) para poder equacionar as forças e aplicar as leis de Newton:
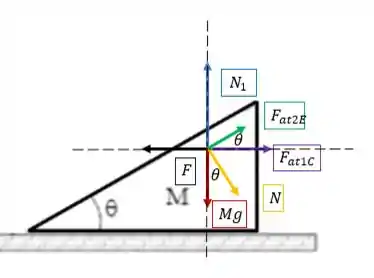
Na vertical temos uma situação de equilíbrio, então as componentes verticais se anulam, daí temos a primeira equação:
A força de atrito entre os blocos está relacionada com a normal entre eles e o coeficiente de atrito estático , e como temos uma expressão para , dessa equação tiramos o valor de
Nosso objetivo é encontrar , mas ela por sua vez está relacionada com a força de atrito cinético entre o bloco e a mesa, e que usa a normal (reação do contato do chão com o bloco ), por isso é importante determinar

Para a direção horizontal a força resultante será igual a , pois esse bloco está se movimentando:
Com o valor da normal que vamos encontrar, podemos achar a força de atrito e achar a força por fim!
Beleza? Mas calma, vamos aos poucos!
Passo 3
Da equação da direção vertical:
Isolando e substituindo :
E por fim resgatando o resultado de do passo 1:
 #chocada
#chocada
Beleza?
Passo 4
Agora vamos usar esse resultado na equação que achamos da direção horizontal:
Trocando e e isolando temos:
E agora usando os resultados de , e obtemos o seguinte:
Podemos agrupar os dois primeiros termos do lado direito:
E por fim podemos ainda agrupar :
E é isso! Esse é o valor máximo da força!
Espero ter ajudado!