Um bloco A, de massa , desce um plano inclinado de ângulo com uma velocidade constante enquanto uma placa B, de massa , está parada sobre o bloco A; esta placa está presa a uma parede no topo do plano inclinado. Assuma que o coeficiente de atrito é o mesmo entre todas as superfícies.
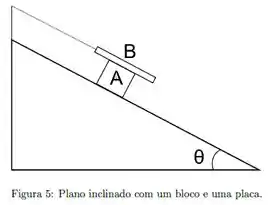
(a) Desenhe o diagrama de forças que agem separadamente nos blocos A e B nas figuras abaixo.
(b) Quais são os pares de forças de ação e reação?
(c) Calcule a forca de atrito entre o bloco A e o bloco B.
(d) Calcule a tensão sobre a corda segurando a placa B.
(e) Calcule a força de atrito entre o bloco A e a superfície do plano inclinado,
(f) Derive o coeficiente de atrito em função das variáveis do problema. Ele depende das massas?
Passo 1
(a) Desenhe o diagrama de forças que agem separadamente nos blocos A e B nas figuras abaixo.
O bloco A está deslizando sobre a rampa e o bloco B está apoiado sobre ele, porém está parado.
Logo, o bloco A terá uma força de atrito com a superfície da rampa e uma força de atrito que a superfície do bloco B exerce sobre A . Ambas são contra o deslizamento de A, ou seja, apontam para cima da rampa.
Além disso, existem as forças normais perpendiculares à cada superfície e a força peso atuando sobre A :
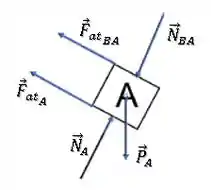
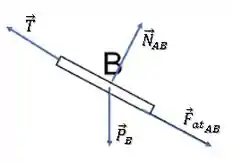
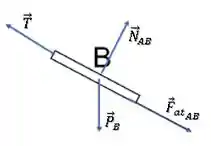
Já o bloco B, terá a força peso para baixo, a força normal que A exerce em B perpendicular à superfície e a força de tração .
Além disso, a força de atrito que A exerce em B , terá sentido contrário à força de atrito que B exerce em A. Portanto, ela apontará para baixo da rampa (A tenta arrastar B para baixo).
Passo 2
(b) Quais são os pares de forças de ação e reação?
Os pares de ação e reação serão as forças normais entre os blocos e as forças de atrito entre os blocos.
O par de ação e reação das normais é:
Enquanto o par de ação e reação das forças de atrito é:
Passo 3
(c) Calcule a forca de atrito entre o bloco A e o bloco B.
A força de atrito cinético é dado pelo produto do coeficiente de atrito cinético com a força normal. No caso do contato entre o bloco A e B, a força normal é ou já que elas tem o mesmo módulo.
Podemos achar essa força normal, fazendo o somatório de forças em B.
Vamos decompor a força peso nas componentes paralela e perpendicular à superfície:
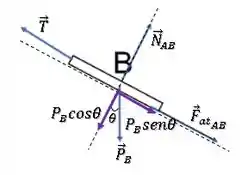
O bloco B está em equilíbrio na direção perpendicular à superfície de contato, então:
Assim, conseguimos a força de atrito entre o bloco A e B:
Passo 4
(d) Calcule a tensão sobre a corda segurando a placa B.
Olhando novamente para as forças em B:
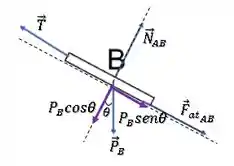
O bloco B está em repouso, logo, as forças na direção paralela à rampa também estão em equilíbrio:
Passo 5
(e) Calcule a força de atrito entre o bloco A e a superfície do plano inclinado,
A força de atritpo entre o bloco A e a rampa será dado por:
Vamos decompor a força peso do bloco A:
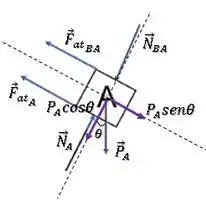
Conseguimos a força normal a partir do somatório de forças na direção perpendicular à superfície da rampa, lembrando que o bloco A está em equilíbrio nessa direção:
A força normal terá o mesmo módulo da força que calculamos no Passo 3:
Logo, a força normal será:
Assim, conseguimos a força de atrito :
Passo 6
(f) Derive o coeficiente de atrito em função das variáveis do problema. Ele depende das massas?
Para encontrar o coeficiente de atrito cinético em função das variáveis do problema, podemos fazer o somatório de forças na direção paralela à rampa em qualquer um dos blocos.
Vamos fazer para o bloco A:
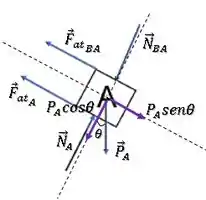
Substituindo os valores:
Resposta
(a)
Bloco A:
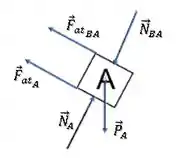
Bloco B:
(b)
(c)
(d)
(e)
(f)