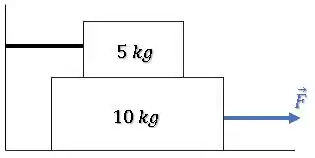
Um bloco de é colocado sobre um de , conforme a figura. Uma força horizontal de é aplicada ao bloco de e o bloco de está preso à parede por uma corda sem massa. O coeficiente de atrito cinético entre todas as superfícies é . A tração na corda é:
A.
B.
C.
D.
E.
Passo 1
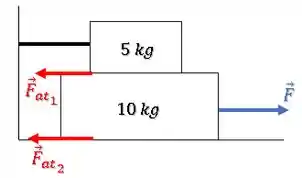
A maior dificuldade desse problema é analisar quais são as forças de atrito e para onde elas apontam.
Quando o bloco de é puxado para a direita pela força , ele vai deslizar sobre a superfície do chão e também sobre a superfície do bloco de , que está preso.
Assim, existe uma força de atrito em cada um desses contatos contrária ao deslizamento desse bloco:
Porém, nosso objetivo é achar a força de tração, então vamos fazer um diagrama do corpo livre para o bloco de e analisar as forças sobre ele.
Passo 2
Pensando agora apenas nas forças sobre o bloco de ...
Se o bloco de exerce uma força de atrito para a esquerda sobre o bloco de , o bloco de exerce uma força de atrito com a mesma intensidade e com o sentido oposto (para a direita):
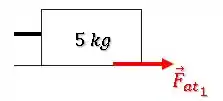
Isso faz sentido, pois quando o bloco de baixo desliza para a direita, ele tenta “arrastar” o bloco de cima também para a direita. Então a força de atrito que o bloco de baixo exerce sobre o bloco de cima é para a direita.
Mas além da força de atrito, temos também uma força Peso para baixo, uma força normal para cima e a força de tração no cabo :
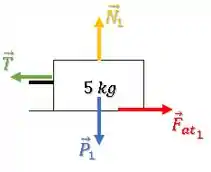
Passo 3
Agora, para descobrir a força de tração , vamos aplicar a Segunda Lei de Newton.
Como o bloco está em equilíbrio (preso à parede), sua aceleração é zero e portanto a força resultante sobre ele é nula:
Passo 4
Se a força resultante sobre o bloco é nula, temos que:
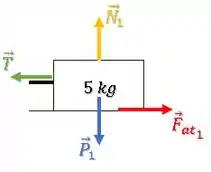
Passo 5
Mas quem é essa força de atrito ?
Bom, a força de atrito cinético é dada por:
E podemos achar o valor da força normal, fazendo o equilíbrio de forças na vertical:
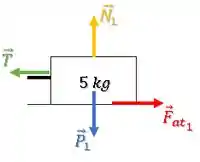
Assim, temos que:
Passo 6
Voltando à expressão da força de tração:
Substituindo os valores numéricos, temos:
Ficamos com a letra B.
Resposta
Letra (B)