Seja a função abaixo definida
- Determine o conjunto dos pontos de continuidade de .
- Determine a função gradiente de .
- Determine o conjunto dos pontos onde é diferenciável.
Passo 1
Faaala, pessoal! Por definição:
Com unitário. Como para , o gradiente está definido como vimos no item , então a função é diferenciável nessa região. Visto que é derivável em qualquer direção.
Passo 2
Contudo, para , precisamos utilizar a definição da derivada direcional. Determinada pela existência do limite abaixo, para unitário e arbitrário e :
Se está fora do círculo de raio centrado na origem, então a função e o limite se anulam. Se está dentro, então:
Contudo, repare que pela restrição de que aponte para dentro do círculo de raio 2, o produto escalar , uma vez que o ângulo entre esses vetores deve ser menor que .
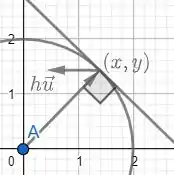
Assim, e:
De forma que o limite não existe. Disto resulta que a função não é diferenciável para os valores , tais que .
Resposta
é diferenciável em .