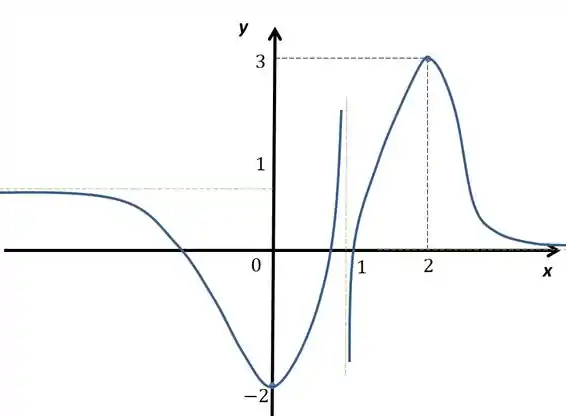
Considere uma função contínua . Com as seguintes propriedades
- é crescente nos intervalos e
- é decrescente nos intervalos e
Responda as questões abaixo
- Esboce o gráfico da função
- Quanto vale ? Quanto vale ?
- Qual o número mínimo de soluções da equação ?
Passo 1
Para fazermos o gráfico primeiro vamos organizar essa parada vamos começar tentando identificar as assíntotas pelo que ele deu. Primeiro vamos as assíntotas horizontais, queremos ver ele deu ali, quais são?
Ou seja temos duas assíntotas horizontais: e
Vamos ver agora as assíntotas verticais, tem algum ponto que vai para ? Repara que temos e fazendo a função ir para infinito, então temos uma assíntota vertical
Onde pela esquerda vai para e pela direita vai para
Passo 2
Vamos ver agora os intervalos de crescimento e decrescimento, mas ele já deu, molezinha hein show de bola
- é crescente nos intervalos e
- é decrescente nos intervalos e
Isso também nos dá os pontos de máximo e mínimo, lembrando que quando vamos do crescente para o decrescente o ponto é de máximo, e quando vamos do decrescente para o crescente o ponto é de mínimo.
Então vamos ter
Precisamos saber o valor da função nesses dois pontos para onde colocar no gráfico. Ele disse que a função é contínua, então vamos ter
Então temos o valor de e o valor de ele deu, que vai ser
Isso já é o suficiente para fazer o gráfico.
Passo 3
Vamos fazer o esboço, primeiro deixa eu desenhar as linhas auxiliares, marcando os máximo e mínimos e as assíntotas.
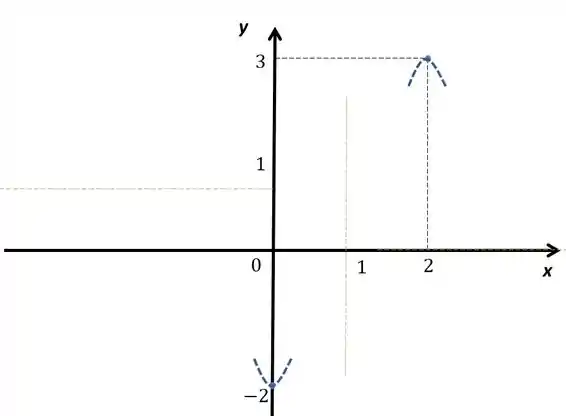
Fazendo o esboço vamos ter algo assim
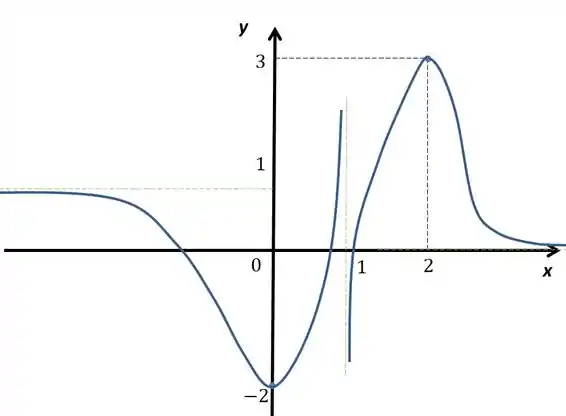
Passo 4
Como já disse ali em cima a função é contínua, então em e vamos ter
Usando os dados que ele deu vamos ter
E está ai as coisas que ele pediu.
Passo 5
Vamos traçar a reta para ver como fica
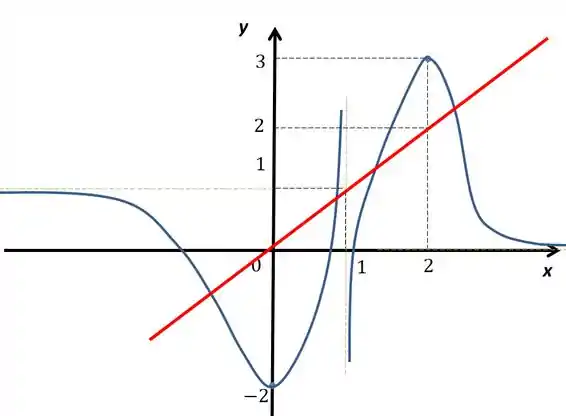
Quantas vezes a reta vermelha corta o gráfico? né? Então o mínimo de soluções que ele tem é