UFRJ – Cálculo 1 – Lista 12 – Questão 1d
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Passo 1
Vamos seguir os passos-a-passos que nos foram pedidos lá no enunciado, beleza?
Passo 2
Domínio
Nossa função não está definida entre , pois não está definida nesses pontos. Assim, nosso domínio é .
Intersecções com os eixos
No eixo , a intersecção ocorre em Como está fora do domínio, então a função não intercepta o eixo . Nossa função não intercepta o eixo , pois isso ocorre quando .
Como não há solução, não há interseção no eixo .
Simetria
Não há simetria no gráfico.
Assíntotas
O gráfico não possui assíntotas horizontais. Isso ocorre pois quando o limite não existe. Em compensação, quando calculamos o limite
Dessa forma, em temos uma assíntota vertical.
Passo 3
Intervalos de crescimento e decrescimento
Derivando a função, temos
quando
Então, está crescendo no intervalo e decrescendo no intervalo .
Valores de máximo e mínimo locais
A função só possui um ponto crítico, que é . Aplicando na nossa função, temos
E é um valor de mínimo local. Não há valor de máximo local
Concavidade e ponto de inflexão
Tirando a segunda derivada da função, temos
é maior que em todos os pontos do domínio. Assim, nossa função possui a concavidade para cima em todos os pontos e não possui ponto de inflexão.
Esboço da curva
Podemos então esboçar graficamente a curva
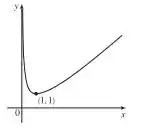
Resposta
