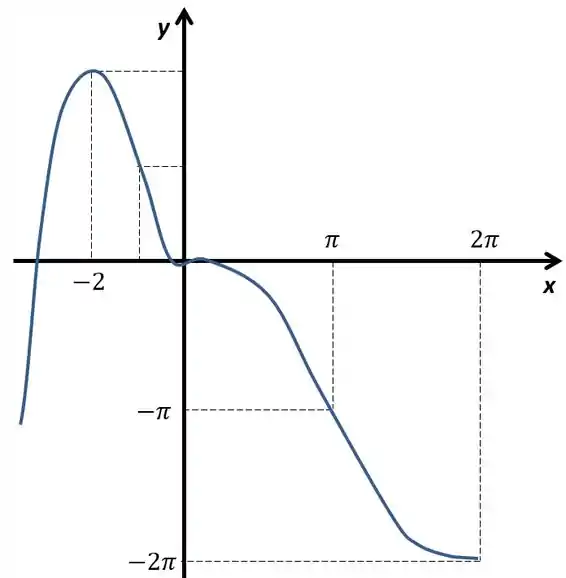
Considere
- é contínua em ? é derivável em ?
- Calcule e
- Determine os pontos críticos de .
- Em quais intervalos é crescente?
- Em quais intervalos é decrescente
- Determine, se houver, os pontos de mínimo local de .
- Determine, se houver, os pontos de máximo local de .
- Em quais intervalos, se houver, o gráfico de é côncavo para cima?
- Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
- Determine, se houver, os pontos de inflexão do gráfico de .
- Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Passo 1
Para sabermos a continuidade dessa função precisamos analisar a função no ponto que pode dar problema que é , como as duas partes de são funções polinomiais ou a função seno elas vão ser contínuas, assim
Como os limites laterais são iguais, vamos ter
E além disso, vamos ter
Logo
E a função vai ser contínua.
Passo 2
Vamos ver agora se ela é derivável, para isso temos que achar as derivadas a direita e a esquerda,
Vamos ter
Como as derivadas laterais são iguais a função vai ser derivável em
Passo 3
Vamos achar os limites que ele pediu
Para esse limite infinito vamos por em evidência, é aquele tipo de limite com polinômio
Passo 4
Vamos começar pelos pontos críticos, para isso devemos achar a derivada de
Vamos igualar essa derivada a , primeiro para
Isso nos diz que
E ambos servem, porque ambos são
Passo 5
Vamos agora ver para
Os valores que o cosseno é um são
Mas aqui só vamos pegar isso porque não está em , ele ignora os extremos.
E o nosso único ponto crítico vai ser
Passo 6
Vamos analisar o sinal da derivada
Na primeira parte vamos ter uma função de segundo grau com duas raízes, a parábola fica algo assim
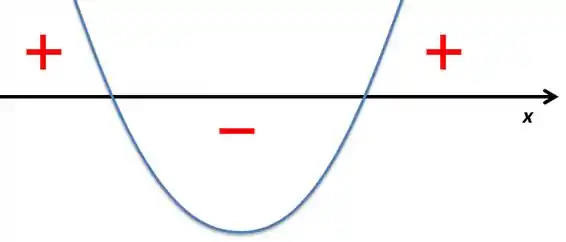
Aqueles pontos são e
Então ela vai ser positiva em
Não vamos pegar porque ele não faz parte do intervalo que a parábola pertence.
Na segunda parte, temos o cosseno,
Como cosseno nunca vai ser maior que ele nunca vai ser positivo, e o intervalo que a função é crescente vai ser
Passo 7
Usando as ideias do passo anterior vamos ter, no primeiro intervalo a derivada vai ser positiva em
Na segunda parte ela vai ser sempre negativa, então a função vai ser decrescente em
Passo 8
Vamos analisar os pontos críticos, são três
Pelo que vimos só em um vai ter troca de sinal da derivada, em , nesse ponto ele vai de para no sinal da derivada, então pelo teste da primeira derivada ele vai ser ponto de máximo local.
Então não temos ponto de mínimo local.
Passo 9
Já vimos que vamos ter um ponto de máximo local, que vai ser onde
Vamos achar o valor de
Passo 10
Para olharmos a concavidade devemos achar a segunda derivada
Vamos analisar o sinal dessa segunda derivada, na primeira parte com
Temos
Dessa forma quando estiver
Ele vai ser côncavo para cima, vamos ver agora a segunda parte dessa derivada
E vamos ter
Sendo o intervalo onde o seno é negativo, dessa forma a função vai ser côncava para cima em
E
Passo 11
Como vimos no passo anterior, o gráfico vai ser côncavo para baixo em
E
Passo 12
Temos trocas de concavidades uma em , uma em e uma em , vamos achar os pontos completos
E os pontos de inflexão vão ser
Passo 13
O gráfico vai ser algo mais ou menos assim, vamos primeiro marcar os pontos de inflexão e o ponto de máximo.
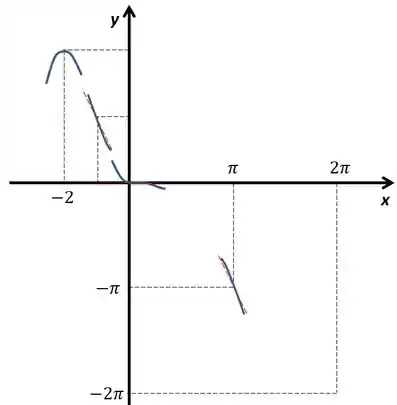
O gráfico vai ficar algo assim
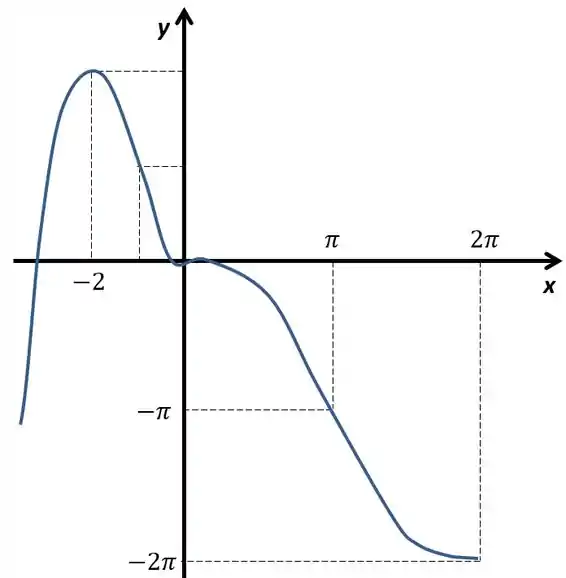
Resposta
- Ela é contínua e derivável
- Não Tem