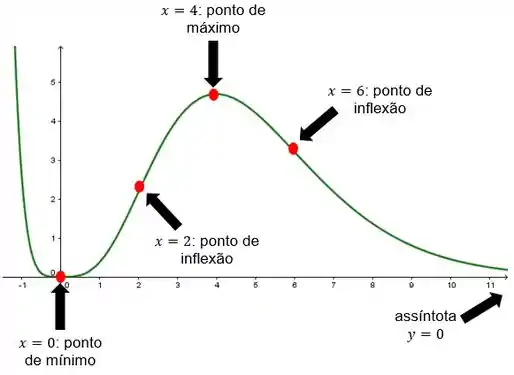
Considere a função .
- Determine os intervalos de crescimento e decrescimento, bem como os pontos críticos. Encontre os pontos de máximo e mínimo locais de .
- Determine os intervalos de concavidade voltada para cima e para baixo, indicando os pontos de inflexão, caso existam.
- Determine as assíntotas horizontais e verticais, caso existam.
- Esboce o gráfico da função, destacando os elementos encontrados nos itens anteriores.
Passo 1
(a)
Vamos começar derivando a . Pela regra do produto:
Igualando a zero:
Como a exponencial é sempre positiva, temos que
Então a função tem 2 pontos críticos, um em e outro em .
Passo 2
Agora, pra descobrir onde a função cresce ou decresce, vamos estudar o sinal da derivada nos intervalos e .
Começando pelo intervalo . Vejamos qual o sinal da derivada em , por exemplo:
No intervalo a derivada é negativa.
Agora vamos pegar um valor entre e , pode ser :
No intervalo a derivada é positiva.
Agora só sobrou o intervalo . É meio intuitivo pensar que, pra muito grande, vamos ter
Mas só pra garantir dá pra conferir, com por exemplo:
No intervalo a derivada é negativa.
Portanto, pelo teste da primeira derivada, decresce no intervalo e cresce no intervalo .
Isso significa que é ponto de mínimo local, e é ponto de máximo local.
Passo 3
(b)
Pra estudar a concavidade, precisamos da segunda derivada. Lembrando que
Derivando de novo, com a regra do produto:
Passo 4
Beleza, agora vamos zerar essa derivada segunda pra achar os candidatos a pontos de inflexão:
Então ou , ou:
Vamos resolver isso por Bhaskara:
Portanto, temos 3 pontos: e .
Passo 5
Agora vejamos o sinal da derivada segunda nos intervalos e .
- Em :
- Em :
- Em :
- Pra :
no intervalo
no intervalo . Ou seja, zerou em , mas não chegou a mudar de sinal passando de pra . Isso significa que não é ponto de inflexão, pois o sinal da derivada segunda não mudou!
no intervalo .
Com valores maiores do que , começa a ficar complicado calcular , ... Mas não precisamos disso, podemos simplesmente dizer que com , temos
no intervalo .
Disso tudo, pelo teste da segunda derivada, concluímos que tem concavidade para cima no intervalo e concavidade para baixo no intervalo .
Os pontos de inflexão são e .
Passo 6
(c)
Agora vamos pras assíntotas.
Assíntotas verticais ocorrem em pontos onde a função não é definida, mas como o domínio da é todo o (não tem nenhum tipo de restrição: raiz quadrada, logaritmo ou divisão), ela não tem assíntotas verticais.
Já pra ver se ela tem assíntotas horizontais, basta calcular os limites no infinito:
Esse limite explodiu pro infinito, então nada de assíntota desse lado. Vamos pro outro limite:
Opa, aqui deu indeterminação. Então vamos fazer o seguinte:
Aplicando l’Hôpital sucessivas vezes:
Não tem jeito, a exponencial sempre ganha!
Enfim, isso significa que , ou seja, o eixo , é uma assíntota horizontal do gráfico da .
Passo 7
(d)
Recapitulando tudo que vimos numa tabela:
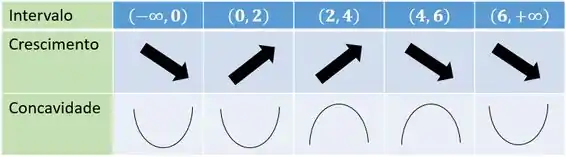
Só ficou faltando na tabela a assíntota quando , e que .
Também temos que e
Essa aproximação de foi bem grosseira mesmo, mas é só pra ter uma noção. Assim sabemos que está ali nos arredores de , e não é tipo , sei lá.
Enfim, a partir disso tudo, tiramos esse lindo gráfico aqui:
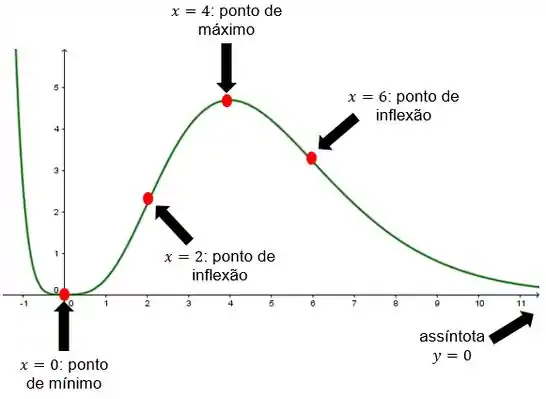
Resposta
(a)
crescimento em
decrescimento em
ponto de mínimo local:
ponto de máximo local:
(b)
concavidade para cima em
concavidade para baixo em
pontos de inflexão: e
(c)
assíntota horizontal:
(d)